\[ \newcommand{\NN}{\mathbb{N}} \newcommand{\CC}{\mathbb{C}} \newcommand{\GG}{\mathbb{G}} \newcommand{\LL}{\mathbb{L}} \newcommand{\PP}{\mathbb{P}} \newcommand{\QQ}{\mathbb{Q}} \newcommand{\RR}{\mathbb{R}} \newcommand{\VV}{\mathbb{V}} \newcommand{\ZZ}{\mathbb{Z}} \newcommand{\FF}{\mathbb{F}} \newcommand{\KK}{\mathbb{K}} \newcommand{\UU}{\mathbb{U}} \newcommand{\EE}{\mathbb{E}} \newcommand{\Aa}{\mathcal{A}} \newcommand{\Bb}{\mathcal{B}} \newcommand{\Cc}{\mathcal{C}} \newcommand{\Dd}{\mathcal{D}} \newcommand{\Ee}{\mathcal{E}} \newcommand{\Ff}{\mathcal{F}} \newcommand{\Gg}{\mathcal{G}} \newcommand{\Hh}{\mathcal{H}} \newcommand{\Ii}{\mathcal{I}} \newcommand{\Jj}{\mathcal{J}} \newcommand{\Kk}{\mathcal{K}} \newcommand{\Ll}{\mathcal{L}} \newcommand{\Mm}{\mathcal{M}} \newcommand{\Nn}{\mathcal{N}} \newcommand{\Oo}{\mathcal{O}} \newcommand{\Pp}{\mathcal{P}} \newcommand{\Qq}{\mathcal{Q}} \newcommand{\Rr}{\mathcal{R}} \newcommand{\Ss}{\mathcal{S}} \newcommand{\Tt}{\mathcal{T}} \newcommand{\Uu}{\mathcal{U}} \newcommand{\Vv}{\mathcal{V}} \newcommand{\Ww}{\mathcal{W}} \newcommand{\Xx}{\mathcal{X}} \newcommand{\Yy}{\mathcal{Y}} \newcommand{\Zz}{\mathcal{Z}} \newcommand{\al}{\alpha} \newcommand{\la}{\lambda} \newcommand{\ga}{\gamma} \newcommand{\Ga}{\Gamma} \newcommand{\La}{\Lambda} \newcommand{\Si}{\Sigma} \newcommand{\si}{\sigma} \newcommand{\be}{\beta} \newcommand{\de}{\delta} \newcommand{\De}{\Delta} \renewcommand{\phi}{\varphi} \renewcommand{\th}{\theta} \newcommand{\om}{\omega} \newcommand{\Om}{\Omega} \renewcommand{\epsilon}{\varepsilon} \newcommand{\Calpha}{\mathrm{C}^\al} \newcommand{\Cbeta}{\mathrm{C}^\be} \newcommand{\Cal}{\text{C}^\al} \newcommand{\Cdeux}{\text{C}^{2}} \newcommand{\Cun}{\text{C}^{1}} \newcommand{\Calt}[1]{\text{C}^{#1}} \newcommand{\lun}{\ell^1} \newcommand{\ldeux}{\ell^2} \newcommand{\linf}{\ell^\infty} \newcommand{\ldeuxj}{{\ldeux_j}} \newcommand{\Lun}{\text{\upshape L}^1} \newcommand{\Ldeux}{\text{\upshape L}^2} \newcommand{\Lp}{\text{\upshape L}^p} \newcommand{\Lq}{\text{\upshape L}^q} \newcommand{\Linf}{\text{\upshape L}^\infty} \newcommand{\lzero}{\ell^0} \newcommand{\lp}{\ell^p} \renewcommand{\d}{\ins{d}} \newcommand{\Grad}{\text{Grad}} \newcommand{\grad}{\text{grad}} \renewcommand{\div}{\text{div}} \newcommand{\diag}{\text{diag}} \newcommand{\pd}[2]{ \frac{ \partial #1}{\partial #2} } \newcommand{\pdd}[2]{ \frac{ \partial^2 #1}{\partial #2^2} } \newcommand{\dotp}[2]{\langle #1,\,#2\rangle} \newcommand{\norm}[1]{|\!| #1 |\!|} \newcommand{\normi}[1]{\norm{#1}_{\infty}} \newcommand{\normu}[1]{\norm{#1}_{1}} \newcommand{\normz}[1]{\norm{#1}_{0}} \newcommand{\abs}[1]{\vert #1 \vert} \newcommand{\argmin}{\text{argmin}} \newcommand{\argmax}{\text{argmax}} \newcommand{\uargmin}[1]{\underset{#1}{\argmin}\;} \newcommand{\uargmax}[1]{\underset{#1}{\argmax}\;} \newcommand{\umin}[1]{\underset{#1}{\min}\;} \newcommand{\umax}[1]{\underset{#1}{\max}\;} \newcommand{\pa}[1]{\left( #1 \right)} \newcommand{\choice}[1]{ \left\{ \begin{array}{l} #1 \end{array} \right. } \newcommand{\enscond}[2]{ \left\{ #1 \;:\; #2 \right\} } \newcommand{\qandq}{ \quad \text{and} \quad } \newcommand{\qqandqq}{ \qquad \text{and} \qquad } \newcommand{\qifq}{ \quad \text{if} \quad } \newcommand{\qqifqq}{ \qquad \text{if} \qquad } \newcommand{\qwhereq}{ \quad \text{where} \quad } \newcommand{\qqwhereqq}{ \qquad \text{where} \qquad } \newcommand{\qwithq}{ \quad \text{with} \quad } \newcommand{\qqwithqq}{ \qquad \text{with} \qquad } \newcommand{\qforq}{ \quad \text{for} \quad } \newcommand{\qqforqq}{ \qquad \text{for} \qquad } \newcommand{\qqsinceqq}{ \qquad \text{since} \qquad } \newcommand{\qsinceq}{ \quad \text{since} \quad } \newcommand{\qarrq}{\quad\Longrightarrow\quad} \newcommand{\qqarrqq}{\quad\Longrightarrow\quad} \newcommand{\qiffq}{\quad\Longleftrightarrow\quad} \newcommand{\qqiffqq}{\qquad\Longleftrightarrow\qquad} \newcommand{\qsubjq}{ \quad \text{subject to} \quad } \newcommand{\qqsubjqq}{ \qquad \text{subject to} \qquad } \]

Sparse Spikes Deconvolution with MUSIC Algorithm

Sparse Spikes Deconvolution with MUSIC Algorithm

This numerical tour explores the use of the MUSIC algorithm to perform sparse deconvolution.

Contents

The MUSIC algorithm was introduced by [Schmidt]. It is closely related to Prony's method [Prony], and is very popular in signal processing [KrimViberg], where it is mostly used for line spectral estimation (i.e. find locations of Diracs in the Fourier spectrum), and we re-formulate here as a problem of finding Diracs' over the temporal domain.

We follow here the exposition of [LiaoFannjiang] who propose a theoretical analysis of the performances of this method. Several related algorithms exists, see for instance [RoyKailathHuaSarkar,DemNeedNg].

Installing toolboxes and setting up the path.

You need to download the following files: signal toolbox and general toolbox.

You need to unzip these toolboxes in your working directory, so that you have toolbox_signal and toolbox_general in your directory.

For Scilab user: you must replace the Matlab comment '%' by its Scilab counterpart '//'.

Recommandation: You should create a text file named for instance numericaltour.sce (in Scilab) or numericaltour.m (in Matlab) to write all the Scilab/Matlab command you want to execute. Then, simply run exec('numericaltour.sce'); (in Scilab) or numericaltour; (in Matlab) to run the commands.

Execute this line only if you are using Matlab.

getd = @(p)path(p,path); % scilab users must *not* execute this

Then you can add the toolboxes to the path.

getd('toolbox_signal/');
getd('toolbox_general/');
ms = 20; % markersize

MUSIC Algorithm

We consider here the problem of recovering a Radon measure \(m_0 \in \Mm(\mathbb{T})\) defined on the torus \(\mathbb{T}=\RR/\ZZ\) from of possibly noisy low-pass measurements \[ y = y_0 + w \qwhereq y_0 = \Phi m_0 \] where \(w\) is the noise term, and so that \( \Phi m \) computes the first \(M+1\) low frequencies of the Fourier transform of \(m\), i.e. \[ \forall \ell \in \{0,\ldots,M\}, \quad (\Phi m)_\ell = \int_{\mathbb{T}} e^{-2\imath\pi x \ell} d m(x). \] We only consider positive frequency because we assume \(m\) is a real measure.

In the following, we consider a discrete measure of the form \(m_0=m_{a_0,x_0}\) where we used the following notation \[ m_{a,x} = \sum_{i=1}^N a_i \de_{x_i} \] where \(a \in \RR^N\) and \(x \in \mathbb{T}^N\).

We thus have \(\Phi m_{a,x} = \Phi_x^M a\) where \[ \Phi_x^{M} = ( e^{-2\imath\pi x_j \ell} )_{0 \leq\ell \leq M, 1 \leq j \leq N} \in \RR^{(M+1) \times N}. \]

Note that \(\Phi_x^{M}\) is a (rectangular) Vandermonde matrix, since \[ \Phi_x^M = (V_{\ga(x)}^M)^* \qwhereq \ga(x) = ( e^{2\imath\pi x_j} )_{j=1}^N \in \CC^N. \]

For \(y \in \RR^M\) and for \(0<L<M\) we denote the Hankel matrix \[ H_y = \begin{pmatrix} y_0 & y_1 & \ldots & y_{M-L} \\ y_1 & y_2 & \ldots & y_{M-L+1} \\ \vdots & \vdots & \ddots & \vdots \\ y_L & y_{L+1} & \ldots & y_M \end{pmatrix} \in \RR^{(L+1) \times (M-L+1) }. \]

Since \(y=\Phi_x^M a+w\), one can check that one has the following factorization \[ H_y = \Phi_x^{L} \diag(a) ( \Phi_x^{M-L} )^* + H_{w}. \]

We suppose that \(\min(L,M-L+1) \geq N\). The fundamental property, which is based on the above factorization, is that \[ s \in \{x_{0,1},\ldots,x_{0,N}\} \quad\Longleftrightarrow\quad \phi_L(s) \in \text{Im}(H_{y_0}) \qwhereq \phi_L(s) = (e^{-2\imath\pi \ell s })_{0 \leq s \leq L} \in \CC^{L+1}. \]

From observations \(y\), we define the following detection function \[ \forall s \in \mathbb{T}, \quad d_y(s) = \norm{ U^{\bot,*} \phi^L(s) }^2, \] where we considered the following SVD factorization \[ H_y = [U, U^\bot] \diag_j(\si_j) [V, V^\bot]^* \] \[ \qwhereq \choice{ U \in \CC^{(L+1) \times N}, U^\bot \in \CC^{(L+1) \times (L+1-N)} \\ V \in \CC^{(M-L+1) \times N}, V^\bot \in \CC^{(M-L+1) \times (M-L+1-N)}. } \]

The detection property can hence be conveniently re-written using this detection function as \[ \{x_{0,1},\ldots,x_{0,N}\} = \enscond{ s }{ d_{y_0}(s)=0 }. \]

Sparse Spikes Deconvolution

We compute here some low frequency measurements.

Number \(M\) of recorded frequency.

M = 18;

Imaging grid, for display purpose.

Q = 1024*4;
z = (0:Q)'/Q;

Input positions \(x_0 \in \mathbb{T}^N\).

x0 = [.1 .4 .5 .7 .9]';

Number \(N\) of spikes.

N = 5;

Input amplitudes \(a_0 \in \RR^N\).

a0 = [.7 -.8 .9 1 -.9]';

Observation operator at position \(x\), i.e. \(\Phi_x\).

Phi = @(x)exp(-2i*pi*(0:M)'*x(:)');

Observations \(y=y_0+w\).

sigma = .15;
w = (randn(M+1,1)+1i*randn(M+1,1)); w = w/norm(w);
y0 = Phi(x0)*a0;
y = y0 + sigma*norm(y0)*w;

Compute the observed low frequency signal \[ f = \frac{1}{2M+1} \sum_{\ell=-P}^P y_\ell e^{2\imath\pi \ell \cdot} \] where we completed the observation using \(y_{-\ell} = \bar y_{\ell}\) since the input measure is real. 

PhiT = @(x)exp(2i*pi*x(:)*(-M:M)) / (2*M+1);
f = real( PhiT(z) * [conj(y(end:-1:2)); y]);

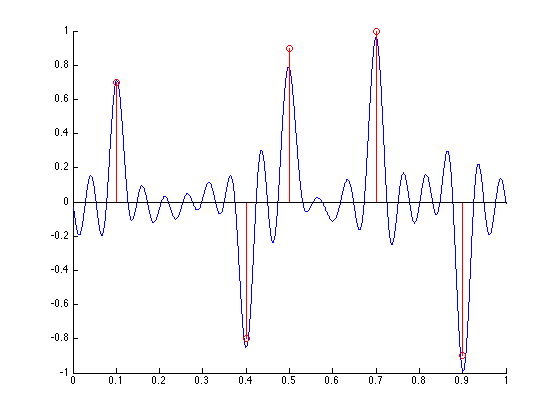
Display the observed signal \(f\), together with the spikes locations.

clf; hold on;
plot(z, f);
stem(x0,a0, 'r');

Noiseless Recovery

We first check the exact recovery when using \(y_0\).

We set here \(L=M/2\), which is a standard choice.

L = M/2;

Build Hankel matrix, one must have min(size(H))>N.

MusicHankel = @(y)hankel(y(1:L),y(L:M));

Compute SVD of \(H_{y_0}\).

[U,S,V] = svd(MusicHankel(y0),0);
S = diag(S);

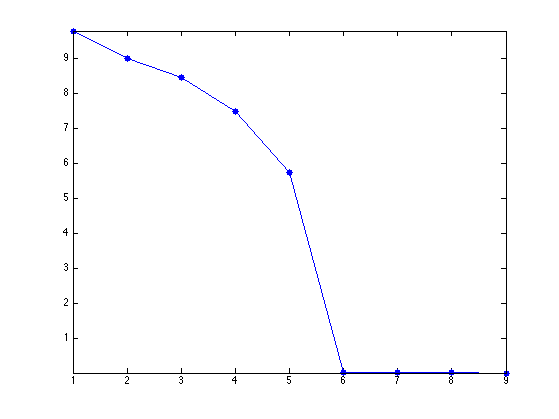
Display the decay of the eigenvalues of \(H_{y_0}\). Since there is no noise, only the \(N\) largest one are non-zero. This is a convenient way to detect \(N\) if it is unknown. 

clf;
plot(S, '.-', 'MarkerSize', ms);
axis tight;

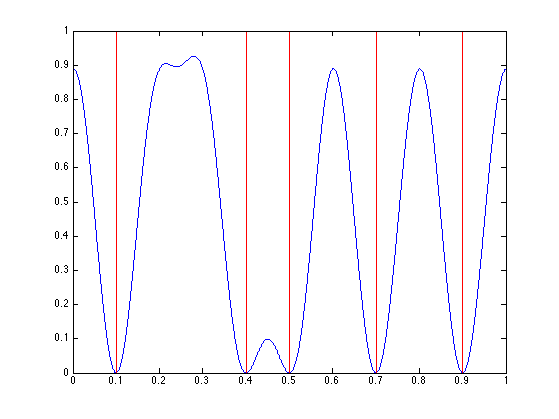
Imaging function \(d_{y_0}\), evaluated on a thin grid \(z \in \mathbb{T}^Q\).

Ubot = U(:,N+1:end);
d = Ubot'*exp(-2i*pi*(0:L-1)'*z(:)');
d = sum(abs(d).^2) / L;

Display \(d\).

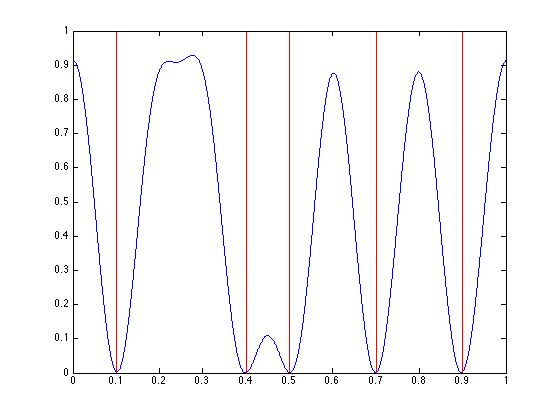
clf; hold on;
plot(z, d, 'b');
stem(x0, 1+x0*0, 'r.');
axis([0 1 0 1]); box on;

Computing the Diracs' Locations by Root Finding

Instead of evaluating the function \(d_{y_0}\) on a thin grid, it is possible to compute directly its zeros using root finding.

Indeed, one has \[ d_y(s) = \norm{ U^{\bot,*} \phi^L(s) }^2 = \sum_j \sum_{\ell,\ell'} \bar U^{\bot}_{\ell,j} U^{\bot}_{\ell',j} z^{\ell-\ell'} \] where we denoted \(z=e^{2\imath\pi s}\).

So the zeros of \(d_y\) are equal to the zeros of the polynomial \(P_y\) that are on the unit circle, where we introduced \[ P_y(z) = \sum_\ell C_\ell z^\ell \qwhereq \choice{ C_\ell = \sum_{j} B_{j,\ell}, \\ B_{j,\cdot} = U_{\cdot,j} \star \bar U_{-\cdot,j}, \\ } \] where \(\star\) is the product of convolution.

This means that \[ \enscond{s}{d_y(s)=0} = \frac{1}{2\pi} \text{Angle}\pa{ \enscond{z}{P_y(z)=0 \qandq \abs{z}=1} } \] where Angle returns the angle of a complex number.

Compute the coefficients \(C\) of the polynomial \(P_{y_0}\).

B = [];
for j=1:size(Ubot,2)
    u = Ubot(:,j);
    v = flipud(conj(u));
    B(:,j) = conv(u,v);
end
C = sum(B,2);

Find its roots.

R = roots(C(end:-1:1));

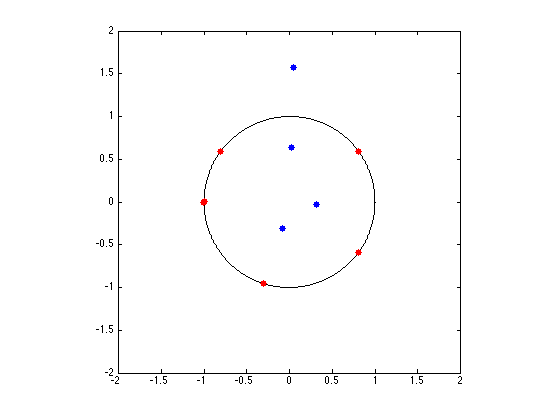
Locate those that are along the circle.

R1 = R(abs( abs(R)-1 )<1e-4);

Display roots.

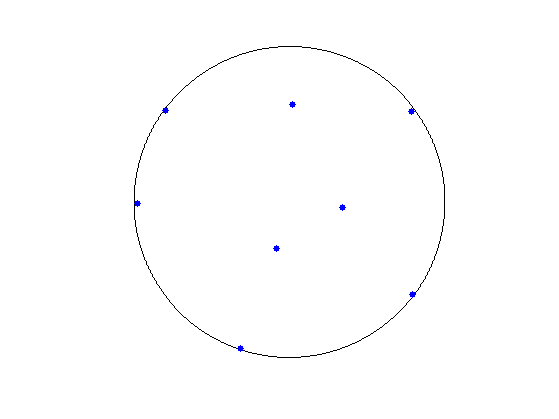
clf; hold on;
plot(exp(2i*pi*z), 'k');
plot(R, 'b.', 'MarkerSize', ms);
plot(R1, 'r.', 'MarkerSize', ms);
axis equal; box on;
axis([-1 1 -1 1]*2);

Sort according to angle, and discard one out of two (because of double roots).

[x1,I] = sort(mod(angle(R1),2*pi)/(2*pi));
x1 = x1(1:2:end);

Compare the found locations with the ground trust.

disp( ['Error (should be 0): ' num2str(norm(x1-x0))] );

Error (should be 0): 3.1113e-09

Noisy Recovery

In practice, one has access to noisy observation \(y=y_0+w\), and one approximates the support \(x\) using the best \(N\) local minima \( \tilde x = \{\tilde x_1,\ldots,\tilde x_N\} \in \mathbb{T}^N \) of \(d_{y}\).

Exercice 1: (check the solution) Compute and display \(d_y\) 

exo1;

Exercice 2: (check the solution) Display the roots of \(P_y\) that are inside the unit disk 

exo2;

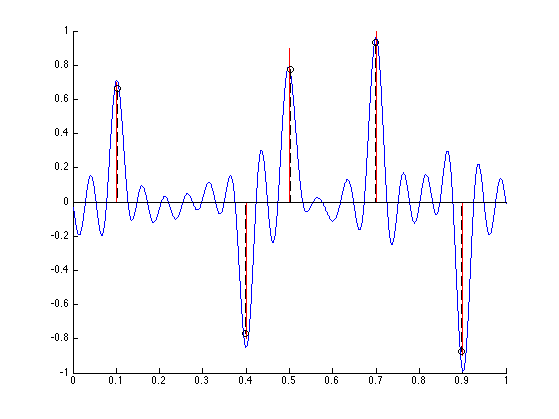
Exercice 3: (check the solution) Keep only the best \(N\) ones, i.e. those that are the closest from the unit circle. We denote those as \(\tilde x \in \mathbb{T}^N\). Recover an approximation \(\tilde a\) of the amplitudes \(a_0\) By solving in least squares (using backslash operator) the system \( \Phi_{\tilde x} \tilde a = y. \) Display the recovered measure \( m_{\tilde a, \tilde x} \). 

exo3;

Exercice 4: (check the solution) Display the evolution of roots as the noise level \(\sigma\) increases. 

exo4;

Bibliography


Copyright (c) 2010 Gabriel Peyre