\[ \newcommand{\NN}{\mathbb{N}} \newcommand{\CC}{\mathbb{C}} \newcommand{\GG}{\mathbb{G}} \newcommand{\LL}{\mathbb{L}} \newcommand{\PP}{\mathbb{P}} \newcommand{\QQ}{\mathbb{Q}} \newcommand{\RR}{\mathbb{R}} \newcommand{\VV}{\mathbb{V}} \newcommand{\ZZ}{\mathbb{Z}} \newcommand{\FF}{\mathbb{F}} \newcommand{\KK}{\mathbb{K}} \newcommand{\UU}{\mathbb{U}} \newcommand{\EE}{\mathbb{E}} \newcommand{\Aa}{\mathcal{A}} \newcommand{\Bb}{\mathcal{B}} \newcommand{\Cc}{\mathcal{C}} \newcommand{\Dd}{\mathcal{D}} \newcommand{\Ee}{\mathcal{E}} \newcommand{\Ff}{\mathcal{F}} \newcommand{\Gg}{\mathcal{G}} \newcommand{\Hh}{\mathcal{H}} \newcommand{\Ii}{\mathcal{I}} \newcommand{\Jj}{\mathcal{J}} \newcommand{\Kk}{\mathcal{K}} \newcommand{\Ll}{\mathcal{L}} \newcommand{\Mm}{\mathcal{M}} \newcommand{\Nn}{\mathcal{N}} \newcommand{\Oo}{\mathcal{O}} \newcommand{\Pp}{\mathcal{P}} \newcommand{\Qq}{\mathcal{Q}} \newcommand{\Rr}{\mathcal{R}} \newcommand{\Ss}{\mathcal{S}} \newcommand{\Tt}{\mathcal{T}} \newcommand{\Uu}{\mathcal{U}} \newcommand{\Vv}{\mathcal{V}} \newcommand{\Ww}{\mathcal{W}} \newcommand{\Xx}{\mathcal{X}} \newcommand{\Yy}{\mathcal{Y}} \newcommand{\Zz}{\mathcal{Z}} \newcommand{\al}{\alpha} \newcommand{\la}{\lambda} \newcommand{\ga}{\gamma} \newcommand{\Ga}{\Gamma} \newcommand{\La}{\Lambda} \newcommand{\Si}{\Sigma} \newcommand{\si}{\sigma} \newcommand{\be}{\beta} \newcommand{\de}{\delta} \newcommand{\De}{\Delta} \renewcommand{\phi}{\varphi} \renewcommand{\th}{\theta} \newcommand{\om}{\omega} \newcommand{\Om}{\Omega} \renewcommand{\epsilon}{\varepsilon} \newcommand{\Calpha}{\mathrm{C}^\al} \newcommand{\Cbeta}{\mathrm{C}^\be} \newcommand{\Cal}{\text{C}^\al} \newcommand{\Cdeux}{\text{C}^{2}} \newcommand{\Cun}{\text{C}^{1}} \newcommand{\Calt}[1]{\text{C}^{#1}} \newcommand{\lun}{\ell^1} \newcommand{\ldeux}{\ell^2} \newcommand{\linf}{\ell^\infty} \newcommand{\ldeuxj}{{\ldeux_j}} \newcommand{\Lun}{\text{\upshape L}^1} \newcommand{\Ldeux}{\text{\upshape L}^2} \newcommand{\Lp}{\text{\upshape L}^p} \newcommand{\Lq}{\text{\upshape L}^q} \newcommand{\Linf}{\text{\upshape L}^\infty} \newcommand{\lzero}{\ell^0} \newcommand{\lp}{\ell^p} \renewcommand{\d}{\ins{d}} \newcommand{\Grad}{\text{Grad}} \newcommand{\grad}{\text{grad}} \renewcommand{\div}{\text{div}} \newcommand{\diag}{\text{diag}} \newcommand{\pd}[2]{ \frac{ \partial #1}{\partial #2} } \newcommand{\pdd}[2]{ \frac{ \partial^2 #1}{\partial #2^2} } \newcommand{\dotp}[2]{\langle #1,\,#2\rangle} \newcommand{\norm}[1]{|\!| #1 |\!|} \newcommand{\normi}[1]{\norm{#1}_{\infty}} \newcommand{\normu}[1]{\norm{#1}_{1}} \newcommand{\normz}[1]{\norm{#1}_{0}} \newcommand{\abs}[1]{\vert #1 \vert} \newcommand{\argmin}{\text{argmin}} \newcommand{\argmax}{\text{argmax}} \newcommand{\uargmin}[1]{\underset{#1}{\argmin}\;} \newcommand{\uargmax}[1]{\underset{#1}{\argmax}\;} \newcommand{\umin}[1]{\underset{#1}{\min}\;} \newcommand{\umax}[1]{\underset{#1}{\max}\;} \newcommand{\pa}[1]{\left( #1 \right)} \newcommand{\choice}[1]{ \left\{ \begin{array}{l} #1 \end{array} \right. } \newcommand{\enscond}[2]{ \left\{ #1 \;:\; #2 \right\} } \newcommand{\qandq}{ \quad \text{and} \quad } \newcommand{\qqandqq}{ \qquad \text{and} \qquad } \newcommand{\qifq}{ \quad \text{if} \quad } \newcommand{\qqifqq}{ \qquad \text{if} \qquad } \newcommand{\qwhereq}{ \quad \text{where} \quad } \newcommand{\qqwhereqq}{ \qquad \text{where} \qquad } \newcommand{\qwithq}{ \quad \text{with} \quad } \newcommand{\qqwithqq}{ \qquad \text{with} \qquad } \newcommand{\qforq}{ \quad \text{for} \quad } \newcommand{\qqforqq}{ \qquad \text{for} \qquad } \newcommand{\qqsinceqq}{ \qquad \text{since} \qquad } \newcommand{\qsinceq}{ \quad \text{since} \quad } \newcommand{\qarrq}{\quad\Longrightarrow\quad} \newcommand{\qqarrqq}{\quad\Longrightarrow\quad} \newcommand{\qiffq}{\quad\Longleftrightarrow\quad} \newcommand{\qqiffqq}{\qquad\Longleftrightarrow\qquad} \newcommand{\qsubjq}{ \quad \text{subject to} \quad } \newcommand{\qqsubjqq}{ \qquad \text{subject to} \qquad } \]

Matrix Completion with Nuclear Norm Minimization

Matrix Completion with Nuclear Norm Minimization

This numerical tour explore the use of convex relaxation to recover low rank matrices from a few measurements.

Contents

Special thanks to Jalal Fadili for useful comments and advices.

Rank and Singular Values

The singular value decomposition of a matrix \(x \in \RR^{n \times n}\) reads \[ x = U S V^* = \sum_{i=0}^{n-1} s_i u_i v_i^* \] where \(S = \diag(s_i)_i\) is the diagonal matrix of singular values that satisfies \[ s_0 \geq \ldots s_{r-1} > 0 \qandq \forall i \geq r, \: s_i=0\] where \(r=\text{rank}(x)\) is the rank of the matrix \(x\). To emphasis the dependancy between the decomposition and \(x\) we will write \(s_i(x), U(x), S(x), V(x)\) when needed.

Note that the matrices \(U,V\) are orthogonal, and the \((u_i)_i\) and \((v_i)_i\) are the columns of these matrices.

Size \(n \times n\) of the matrix.

n = 100;

Rank \(r\) of the matrix.

r = 10;

Generate a random matrix \(x_0 \in \RR^{n \times n} \) of rank \(r\), as the product of Gaussian vectors.

x0 = randn(n,r)*randn(r,n);

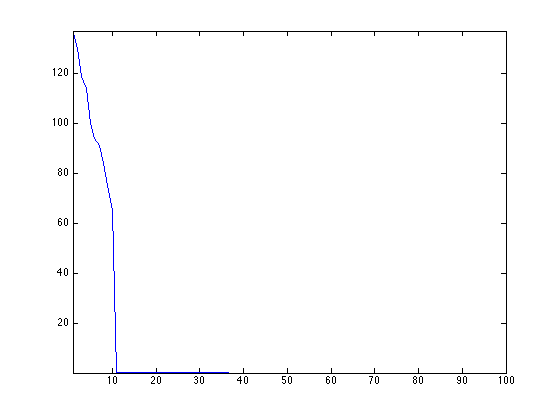
Display the singular values. Only \(r\) are non zero, and they are clustered around the value \(n\).

plot(svd(x0), '.-');
axis tight;

Matrix Completion

We consider here a simple measurement operator \(\Phi : \RR^{n \times n} \rightarrow \RR^P\) that retains only a sub-set of the entries of the matix. \[ \Phi x = ( x_i )_{i \in I} \] where \(\abs{I}=P\) is the set of extracted indexes.

One can of course consider other linear measurement operators.

Number \(P\) of measurements.

P = round( n*log(n)*r*1 );

We use here a set of random sampling locations.

I = randperm(n*n); I = I(1:P); I = I(:);

Measurement operator and its adjoint.

Phi  = @(x)x(I);
PhiS= @(y)reshape( accumarray(I, y, [n*n 1], @sum), [n n]);

Measurement \(y=\Phi x_0\).

y = Phi(x0);

The low-rank matrix completion corresponds to the following non-convex minimization. \[ x^{\star} \in \uargmin{\Phi x = y} \text{rank}(x). \]

Noiseless Completion using Douglas Rachford

To obtain fast algorithm, it is possible to convexify the objective function and use the nuclear norm \( \norm{x}_{\star} \) \[ x^{\star} \in \umin{\Phi x = y} \norm{x}_{\star} = \sum_i s_i(x) \] This is a convex problem, that can be solved efficiently, as we show next.

It is shown in

The Power of Convex Relaxation: Near-Optimal Matrix Completion E. J. Candes and T. Tao, IEEE Trans. Inform. Theory, 56(5), 2053-2080, 2009.

that if the columns of \(U(x_0)\) and \(V(x_0)\) have a small enough \(\ell^\infty\) norm, and if \(P \geq C r n \log(n)\) for some absolute constant \(C\) then \(x^\star=x_0\).

This minimization can be written as \[ \umin{ x } F(x) + G(x) \qwhereq \choice{ F(x) = i_{\Cc}(x), \\ G(x) = \norm{x}_{\star}. } \] where \(\Cc = \enscond{x}{\Phi x =y}\).

One can solve this problem using the Douglas-Rachford iterations \[ \tilde x_{k+1} = \pa{1-\frac{\mu}{2}} \tilde x_k + \frac{\mu}{2} \text{rPox}_{\gamma G}( \text{rProx}_{\gamma F}(\tilde x_k) ) \qandq x_{k+1} = \text{Prox}_{\gamma F}(\tilde x_{k+1},) \]

We have use the following definition for the proximal and reversed-proximal mappings: \[ \text{rProx}_{\gamma F}(x) = 2\text{Prox}_{\gamma F}(x)-x \] \[ \text{Prox}_{\gamma F}(x) = \uargmin{y} \frac{1}{2}\norm{x-y}^2 + \ga F(y). \]

One can show that for any value of \(\gamma>0\), any \( 0 < \mu < 2 \), and any \(\tilde x_0\), \(x_k \rightarrow x^\star\) which is a solution of the minimization of \(F+G\).

\[ \text{Prox}_{\gamma F}(x) = \uargmin{y} \frac{1}{2}\norm{x-y}^2 + \ga F(y). \]

The proximal operator of \(F\) is the orthogonal projection on \(\Cc\). It is computed as \[ \text{Prox}_{\ga F}(x) = x + \Phi^*(y-\Phi x). \] 

ProxF = @(x,gamma)x + PhiS(y-Phi(x));

The proximal operator of \(G\) is the soft thresholding of the singular values \[ \text{Prox}_{\ga F}(x) = U(x) \rho_\la( S(x) ) V(x)^* \] where, for \( S=\text{diag}(s_i)_i \) \[ \rho_\la(S) = \diag\pa{ \max(0,1-\la/\abs{s_i}) s_i }_i. \]

Define \(\rho_\la\) as a diagonal operator.

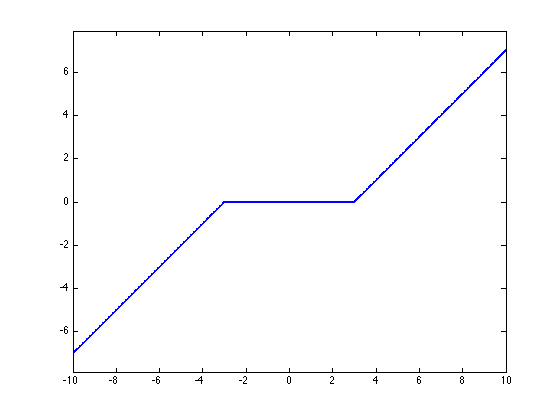
SoftThresh = @(x,gamma)max(0,1-gamma./max(abs(x),1e-10)).*x;

Display it in 1-D.

t = linspace(-10,10,1000);
h = plot(t, SoftThresh(t,3)); axis tight; axis equal;
set(h, 'LineWidth', 2);

Define the proximal mapping \(\text{Prox}_{\ga F}\).

prod = @(a,b,c)a*b*c;
SoftThreshDiag = @(a,b,c,gamma)a*diag(SoftThresh(diag(b),gamma))*c';
ProxG = @(x,gamma)apply_multiple_ouput(@(a,b,c)SoftThreshDiag(a,b,c,gamma), @svd, x);

Compute the reversed prox operators.

rProxF = @(x,gamma)2*ProxF(x,gamma)-x;
rProxG = @(x,gamma)2*ProxG(x,gamma)-x;

Value for the \(0 < \mu < 2\) and \(\gamma>0\) parameters. You can use other values, this might speed up the convergence.

mu = 1;
gamma = 1;

Exercice 1: (check the solution) Implement the Douglas-Rachford iterative algorithm. Keep track of the evolution of the nuclear norm \(G(x_k)\). 

exo1;

In this case, the matrix is recovered exactly, \(A^\star=A_0\).

disp(['|A-A_0|/|A_0| = ' num2str(norm(x-x0)/norm(x), 2)]);

|A-A_0|/|A_0| = 4e-07

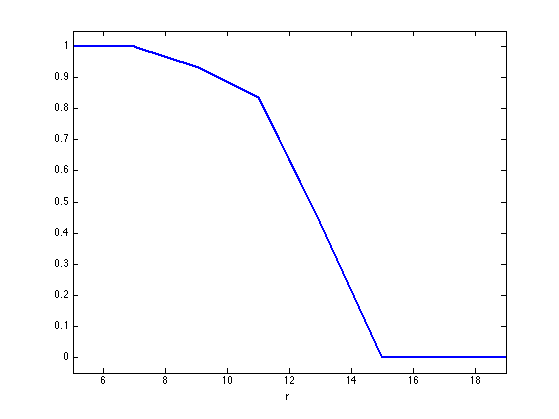
Exercice 2: (check the solution) Compute, for several value of rank \(r\), an empirical estimate of the ratio of rank-\(r\) random matrice than are exactly recovered using nuclear norm minimization. 

exo2;

Noisy Completion using Forward-Backward

In the case where \(x_0\) does not have low rank but a fast decreasing set of singular values \( (s_i(x_0))_i \), and if one has noisy observations \(y = \Phi x_0 + w\), where \(w \in \RR^P\) is some noise perturbation, then it makes sense to consider a Lagrangian minimization \[ \umin{x \in \RR^{n \times n}} \frac{1}{2}\norm{y-\Phi x}^2 + \la \norm{x}_{\star} \] where \(\la>0\) controls the sparsity of the singular values of the solution.

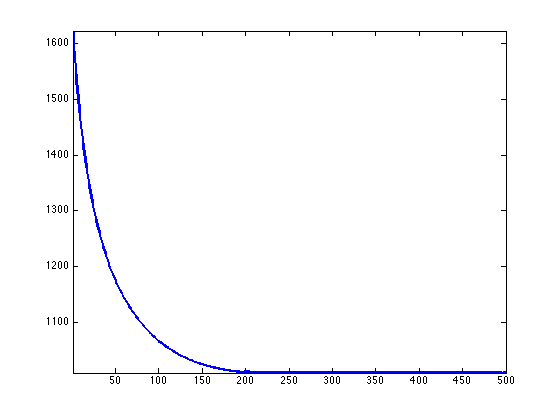
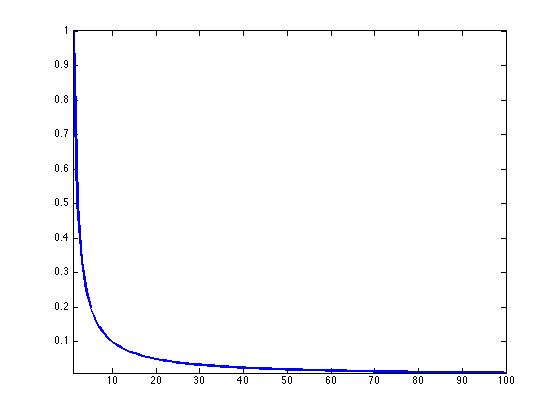
Construct a matrix with decaying singular values.

alpha = 1;
[U,R] = qr(randn(n));
[V,R] = qr(randn(n));
S = (1:n).^(-alpha);
x0 = U*diag(S)*V';

Display the spectrum.

clf;
h = plot(S); axis tight;
set(h, 'LineWidth', 2);

Number of measurements.

P = n*n/4;

Measurement operator.

I = randperm(n*n); I = I(1:P); I = I(:);
Phi  = @(x)x(I);
PhiS= @(y)reshape( accumarray(I, y, [n*n 1], @sum), [n n]);

Noise level.

sigma = std(x0(:))/5;

Measurements \(y=\Phi x_0 + w\) where \(w \in \RR^P\) is a Gaussian white noise.

y = Phi(x0)+sigma*randn(P,1);

It is possible to find a minimizer of the Lagrangian minimization problem using the forward-backward method: \[ x_{k+1} = \text{Prox}_{\ga \lambda G}\pa{ x_k - \ga\Phi^*(\Phi x_k - y) }. \] where \(\ga < 2/\norm{\Phi^* \Phi} = 2. \)

Value for \(\lambda\).

lambda = .01;

Exercice 3: (check the solution) Implement the forward-backward method, monitor the decay of the enrgy minimized by the algorithm. 

exo3;

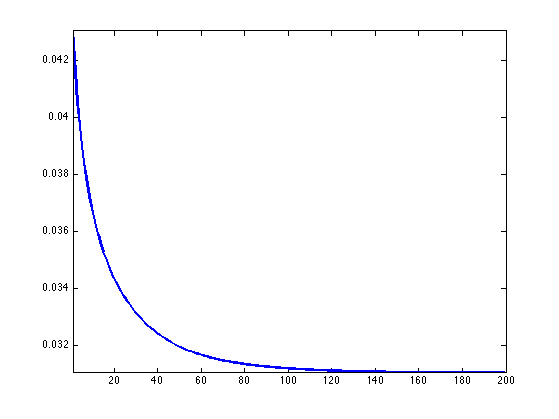
Exercice 4: (check the solution) Plot the error \(\norm{x^\star-x_0}/\norm{x_0}\) as a function of the mutiplier \(\lambda\). 

exo4;


Copyright (c) 2010 Gabriel Peyre