\[ \newcommand{\NN}{\mathbb{N}} \newcommand{\CC}{\mathbb{C}} \newcommand{\GG}{\mathbb{G}} \newcommand{\LL}{\mathbb{L}} \newcommand{\PP}{\mathbb{P}} \newcommand{\QQ}{\mathbb{Q}} \newcommand{\RR}{\mathbb{R}} \newcommand{\VV}{\mathbb{V}} \newcommand{\ZZ}{\mathbb{Z}} \newcommand{\FF}{\mathbb{F}} \newcommand{\KK}{\mathbb{K}} \newcommand{\UU}{\mathbb{U}} \newcommand{\EE}{\mathbb{E}} \newcommand{\Aa}{\mathcal{A}} \newcommand{\Bb}{\mathcal{B}} \newcommand{\Cc}{\mathcal{C}} \newcommand{\Dd}{\mathcal{D}} \newcommand{\Ee}{\mathcal{E}} \newcommand{\Ff}{\mathcal{F}} \newcommand{\Gg}{\mathcal{G}} \newcommand{\Hh}{\mathcal{H}} \newcommand{\Ii}{\mathcal{I}} \newcommand{\Jj}{\mathcal{J}} \newcommand{\Kk}{\mathcal{K}} \newcommand{\Ll}{\mathcal{L}} \newcommand{\Mm}{\mathcal{M}} \newcommand{\Nn}{\mathcal{N}} \newcommand{\Oo}{\mathcal{O}} \newcommand{\Pp}{\mathcal{P}} \newcommand{\Qq}{\mathcal{Q}} \newcommand{\Rr}{\mathcal{R}} \newcommand{\Ss}{\mathcal{S}} \newcommand{\Tt}{\mathcal{T}} \newcommand{\Uu}{\mathcal{U}} \newcommand{\Vv}{\mathcal{V}} \newcommand{\Ww}{\mathcal{W}} \newcommand{\Xx}{\mathcal{X}} \newcommand{\Yy}{\mathcal{Y}} \newcommand{\Zz}{\mathcal{Z}} \newcommand{\al}{\alpha} \newcommand{\la}{\lambda} \newcommand{\ga}{\gamma} \newcommand{\Ga}{\Gamma} \newcommand{\La}{\Lambda} \newcommand{\Si}{\Sigma} \newcommand{\si}{\sigma} \newcommand{\be}{\beta} \newcommand{\de}{\delta} \newcommand{\De}{\Delta} \renewcommand{\phi}{\varphi} \renewcommand{\th}{\theta} \newcommand{\om}{\omega} \newcommand{\Om}{\Omega} \renewcommand{\epsilon}{\varepsilon} \newcommand{\Calpha}{\mathrm{C}^\al} \newcommand{\Cbeta}{\mathrm{C}^\be} \newcommand{\Cal}{\text{C}^\al} \newcommand{\Cdeux}{\text{C}^{2}} \newcommand{\Cun}{\text{C}^{1}} \newcommand{\Calt}[1]{\text{C}^{#1}} \newcommand{\lun}{\ell^1} \newcommand{\ldeux}{\ell^2} \newcommand{\linf}{\ell^\infty} \newcommand{\ldeuxj}{{\ldeux_j}} \newcommand{\Lun}{\text{\upshape L}^1} \newcommand{\Ldeux}{\text{\upshape L}^2} \newcommand{\Lp}{\text{\upshape L}^p} \newcommand{\Lq}{\text{\upshape L}^q} \newcommand{\Linf}{\text{\upshape L}^\infty} \newcommand{\lzero}{\ell^0} \newcommand{\lp}{\ell^p} \renewcommand{\d}{\ins{d}} \newcommand{\Grad}{\text{Grad}} \newcommand{\grad}{\text{grad}} \renewcommand{\div}{\text{div}} \newcommand{\diag}{\text{diag}} \newcommand{\pd}[2]{ \frac{ \partial #1}{\partial #2} } \newcommand{\pdd}[2]{ \frac{ \partial^2 #1}{\partial #2^2} } \newcommand{\dotp}[2]{\langle #1,\,#2\rangle} \newcommand{\norm}[1]{|\!| #1 |\!|} \newcommand{\normi}[1]{\norm{#1}_{\infty}} \newcommand{\normu}[1]{\norm{#1}_{1}} \newcommand{\normz}[1]{\norm{#1}_{0}} \newcommand{\abs}[1]{\vert #1 \vert} \newcommand{\argmin}{\text{argmin}} \newcommand{\argmax}{\text{argmax}} \newcommand{\uargmin}[1]{\underset{#1}{\argmin}\;} \newcommand{\uargmax}[1]{\underset{#1}{\argmax}\;} \newcommand{\umin}[1]{\underset{#1}{\min}\;} \newcommand{\umax}[1]{\underset{#1}{\max}\;} \newcommand{\pa}[1]{\left( #1 \right)} \newcommand{\choice}[1]{ \left\{ \begin{array}{l} #1 \end{array} \right. } \newcommand{\enscond}[2]{ \left\{ #1 \;:\; #2 \right\} } \newcommand{\qandq}{ \quad \text{and} \quad } \newcommand{\qqandqq}{ \qquad \text{and} \qquad } \newcommand{\qifq}{ \quad \text{if} \quad } \newcommand{\qqifqq}{ \qquad \text{if} \qquad } \newcommand{\qwhereq}{ \quad \text{where} \quad } \newcommand{\qqwhereqq}{ \qquad \text{where} \qquad } \newcommand{\qwithq}{ \quad \text{with} \quad } \newcommand{\qqwithqq}{ \qquad \text{with} \qquad } \newcommand{\qforq}{ \quad \text{for} \quad } \newcommand{\qqforqq}{ \qquad \text{for} \qquad } \newcommand{\qqsinceqq}{ \qquad \text{since} \qquad } \newcommand{\qsinceq}{ \quad \text{since} \quad } \newcommand{\qarrq}{\quad\Longrightarrow\quad} \newcommand{\qqarrqq}{\quad\Longrightarrow\quad} \newcommand{\qiffq}{\quad\Longleftrightarrow\quad} \newcommand{\qqiffqq}{\qquad\Longleftrightarrow\qquad} \newcommand{\qsubjq}{ \quad \text{subject to} \quad } \newcommand{\qqsubjqq}{ \qquad \text{subject to} \qquad } \]

Active Contours using Parameteric Curves

Active Contours using Parameteric Curves

This tour explores image segmentation using parametric active contours.

Contents

Installing toolboxes and setting up the path.

You need to download the following files: signal toolbox, general toolbox and graph toolbox.

You need to unzip these toolboxes in your working directory, so that you have toolbox_signal, toolbox_general and toolbox_graph in your directory.

For Scilab user: you must replace the Matlab comment '%' by its Scilab counterpart '//'.

Recommandation: You should create a text file named for instance numericaltour.sce (in Scilab) or numericaltour.m (in Matlab) to write all the Scilab/Matlab command you want to execute. Then, simply run exec('numericaltour.sce'); (in Scilab) or numericaltour; (in Matlab) to run the commands.

Execute this line only if you are using Matlab.

getd = @(p)path(p,path); % scilab users must *not* execute this

Then you can add the toolboxes to the path.

getd('toolbox_signal/');
getd('toolbox_general/');
getd('toolbox_graph/');

Parameteric Curves

In this tours, the active contours are represented using parametric curve \( \ga : [0,1] \rightarrow \RR^2 \).

This curve is discretized using a piewise linear curve with \(p\) segments, and is stored as a complex vector of points in the plane \(\ga \in \CC^p\).

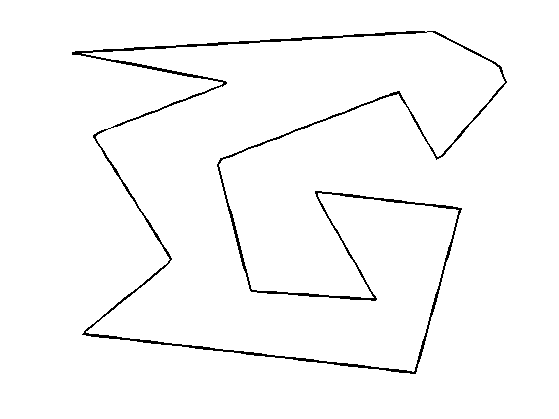
Initial polygon.

gamma0 = [0.78 0.14 0.42 0.18 0.32 0.16 0.75 0.83 0.57 0.68 0.46 0.40 0.72 0.79 0.91 0.90]' + ...
     1i* [0.87 0.82 0.75 0.63 0.34 0.17 0.08 0.46 0.50 0.25 0.27 0.57 0.73 0.57 0.75 0.79]';

Number of points of the discrete curve.

p = 256;

Shortcut to re-sample a curve according to arc length.

curvabs = @(gamma)[0;cumsum( 1e-5 + abs(gamma(1:end-1)-gamma(2:end)) )];
resample1 = @(gamma,d)interp1(d/d(end),gamma,(0:p-1)'/p, 'linear');
resample = @(gamma)resample1( [gamma;gamma(1)], curvabs( [gamma;gamma(1)] ) );

Initial curve \( \ga_1(t) \).

gamma1 = resample(gamma0);

Display the initial curve.

clf;
h = plot(gamma1([1:end 1]), 'k');
set(h, 'LineWidth', 2); axis('tight'); axis('off');

Shortcut for forward and backward finite differences.

BwdDiff = @(c)c - c([end 1:end-1]);
FwdDiff = @(c)c([2:end 1]) - c;
dotp = @(c1,c2)real(c1.*conj(c2));

The tangent to the curve is computed as \[ t_\ga(s) = \frac{\ga'(t)}{\norm{\ga'(t)}} \] and the normal is \( n_\ga(t) = t_\ga(t)^\bot. \)

Shortcut to compute the tangent and the normal to a curve.

normalize = @(v)v./max(abs(v),eps);
tangent = @(gamma)normalize( FwdDiff(gamma) );
normal = @(gamma)-1i*tangent(gamma);

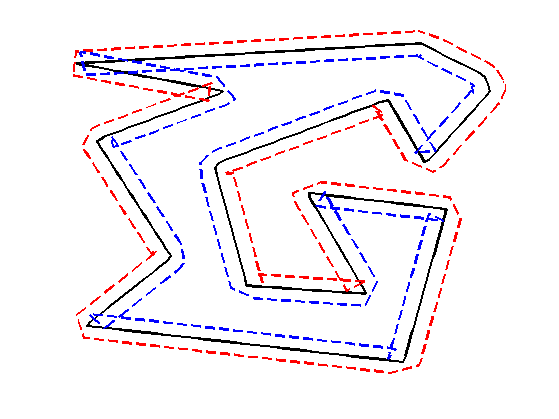
Move the curve in the normal direction, by computing \( \ga_1(t) \pm \delta n_{\ga_1}(t) \).

delta = .03;
gamma2 = gamma1 + delta * normal(gamma1);
gamma3 = gamma1 - delta * normal(gamma1);

Display the curves.

clf;
hold on;
h = plot(gamma1([1:end 1]), 'k'); set(h, 'LineWidth', 2);
h = plot(gamma2([1:end 1]), 'r--'); set(h, 'LineWidth', 2);
h = plot(gamma3([1:end 1]), 'b--'); set(h, 'LineWidth', 2);
axis('tight'); axis('off');

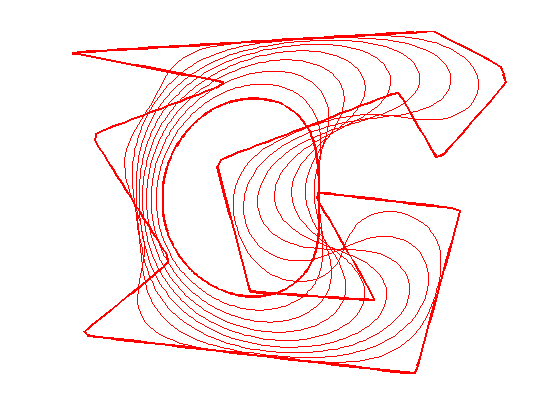
Evolution by Mean Curvature

A curve evolution is a series of curves \( s \mapsto \ga_s \) indexed by an evolution parameter \(s \geq 0\). The intial curve \(\ga_0\) for \(s=0\) is evolved, usually by minizing some energy \(E(\ga)\) in a gradient descent \[ \frac{\partial \ga_s}{\partial s} = \nabla E(\ga_s). \]

Note that the gradient of an energy is defined with respect to the curve-dependent inner product \[ \dotp{a}{b} = \int_0^1 \dotp{a(t)}{b(t)} \norm{\ga'(t)} d t. \] The set of curves can thus be thought as being a Riemannian surface.

The simplest evolution is the mean curvature evolution. It corresponds to minimization of the curve length \[ E(\ga) = \int_0^1 \norm{\ga'(t)} d t \]

The gradient of the length is \[ \nabla E(\ga)(t) = -\kappa_\ga(t) n_\ga(t) \] where \( \kappa_\ga \) is the curvature, defined as \[ \kappa_\ga(t) = \frac{1}{\norm{\ga'(t)}} \dotp{ t_\ga'(t) }{ n_\ga(t) } . \]

Shortcut for normal times curvature \( \kappa_\ga(t) n_\ga(t) \).

normalC = @(gamma)BwdDiff(tangent(gamma)) ./ abs( FwdDiff(gamma) );

Time step for the evolution. It should be very small because we use an explicit time stepping and the curve has strong curvature.

dt = 0.001 / 100;

Number of iterations.

Tmax = 3 / 100;
niter = round(Tmax/dt);

Initialize the curve for \(s=0\).

gamma = gamma1;

Evolution of the curve.

gamma = gamma + dt * normalC(gamma);

To stabilize the evolution, it is important to re-sample the curve so that it is unit-speed parametrized. You do not need to do it every time step though (to speed up). 

gamma = resample(gamma);

Exercice 1: (check the solution) Perform the curve evolution. You need to resample it a few times. 

exo1;

Geodesic Active Contours

Geodesic active contours minimize a weighted length \[ E(\ga) = \int_0^1 W(\ga(t)) \norm{\ga'(t)} d t, \] where \(W(x)>0\) is the geodesic metric, that should be small in areas where the image should be segmented.

Create a synthetic weight \(W(x)\).

n = 200;
nbumps = 40;
theta = rand(nbumps,1)*2*pi;
r = .6*n/2; a = [.62*n .6*n];
x = round( a(1) + r*cos(theta) );
y = round( a(2) + r*sin(theta) );
W = zeros(n); W( x + (y-1)*n ) = 1;
W = perform_blurring(W,10);
W = rescale( -min(W,.05), .3,1);

Display the metric.

clf;
imageplot(W);

Pre-compute the gradient \(\nabla W(x)\) of the metric.

options.order = 2;
G = grad(W, options);
G = G(:,:,1) + 1i*G(:,:,2);

Shortcut to evaluate the gradient and the potential along a curve.

EvalG = @(gamma)interp2(1:n,1:n, G, imag(gamma), real(gamma));
EvalW = @(gamma)interp2(1:n,1:n, W, imag(gamma), real(gamma));

Create a circular curve \(\ga_0\).

r = .98*n/2;
p = 128; % number of points on the curve
theta = linspace(0,2*pi,p+1)'; theta(end) = [];
gamma0 = n/2*(1+1i) +  r*(cos(theta) + 1i*sin(theta));

Initialize the curve at time \(t=0\) with a circle.

gamma = gamma0;

For this experiment, the time step should be larger, because the curve is in \([1,n] \times [1,n]\).

dt = 1;

Number of iterations.

Tmax = 5000;
niter = round(Tmax/dt);

Display the curve on the back ground;

lw = 2;
clf; hold on;
imageplot(W);
h = plot(imag(gamma([1:end 1])),real(gamma([1:end 1])), 'r');
set(h, 'LineWidth', lw);
axis('ij');

The gradient of the energy is \[ \nabla E(\ga) = -W(\ga(t)) \kappa_\ga(t) n_\ga(t) + \dotp{\nabla W(\ga(t))}{ n_\ga(t) } n_\ga(t). \]

Evolution of the curve according to this gradient.

N = normal(gamma);
g = - EvalW(gamma).*normalC(gamma) + dotp(EvalG(gamma), N) .* N;
gamma = gamma - dt*g;

To avoid the curve from being poorly sampled, it is important to re-sample it evenly.

gamma = resample( gamma );

Exercice 2: (check the solution) Perform the curve evolution. 

exo2;

Medical Image Segmentation

One can use a gradient-based metric to perform edge detection in medical images.

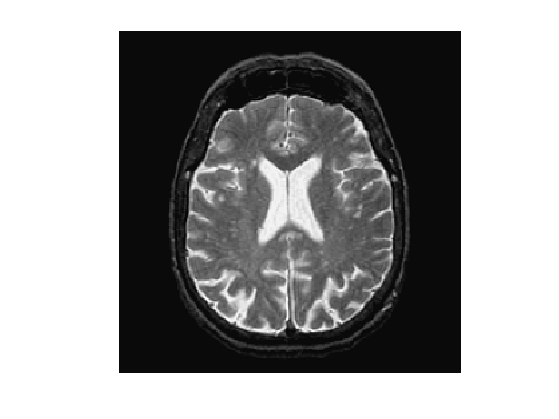
Load an image \(f\).

n = 256;
f = rescale( sum(load_image('cortex', n), 3 ) );

Display.

clf;
imageplot(f);

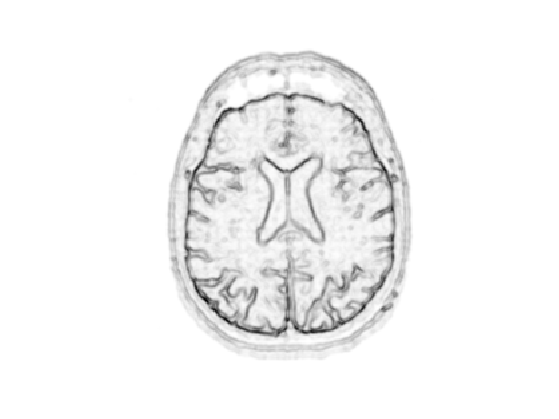
An edge detector metric can be defined as a decreasing function of the gradient magnitude. \[ W(x) = \psi( d \star h_a(x) ) \qwhereq d(x) = \norm{\nabla f(x)}. \] where \(h_a\) is a blurring kernel of width \(a>0\).

Compute the magnitude of the gradient.

options.order = 2;
G = grad(f,options);
d = sqrt(sum(G.^2,3));

Blur it by \(h_a\).

a = 3;
d = perform_blurring(d,a);

Compute a decreasing function of the gradient to define \(W\).

d = min(d,.4);
W = rescale(-d,.8,1);

Display it.

clf;
imageplot(W);

Number of points.

p = 128;

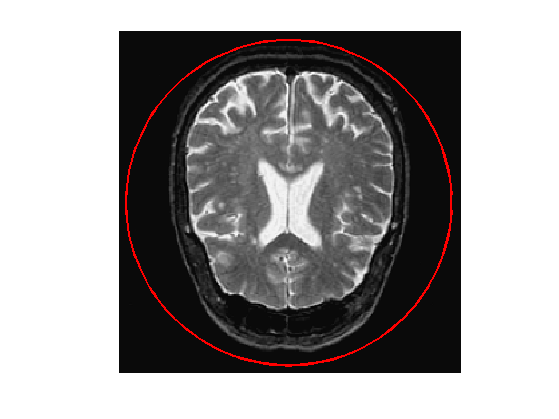
Exercice 3: (check the solution) Create an initial circle \(\gamma_0\) of \(p\) points. 

exo3;

Step size.

dt = 2;

Number of iterations.

Tmax = 9000;
niter = round(Tmax/dt);

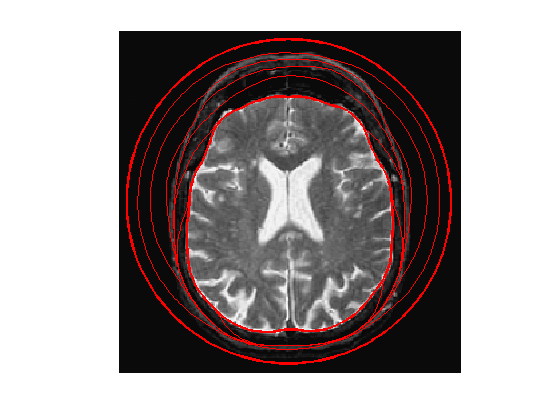
Exercice 4: (check the solution) Perform the curve evolution. 

exo4;

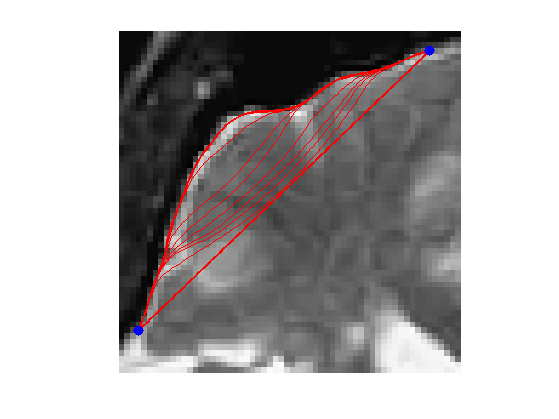
Evolution of a Non-closed Curve

It is possible to perform the evolution of a non-closed curve by adding boundary constraint \[ \ga(0)=x_0 \qandq \ga(1)=x_1. \]

In this case, the algorithm find a local minimizer of the geodesic distance between the two points.

Note that a much more efficient way to solve this problem is to use the Fast Marching algorithm to find the global minimizer of the geodesic length.

Load an image \(f\).

n = 256;
f = rescale( sum(load_image('cortex', n), 3 ) );
f = f(46:105,61:120);
n = size(f,1);

Display.

clf;
imageplot(f);

Exercice 5: (check the solution) Compute an edge attracting criterion \(W(x)>0\), that is small in area of strong gradient. 

exo5;

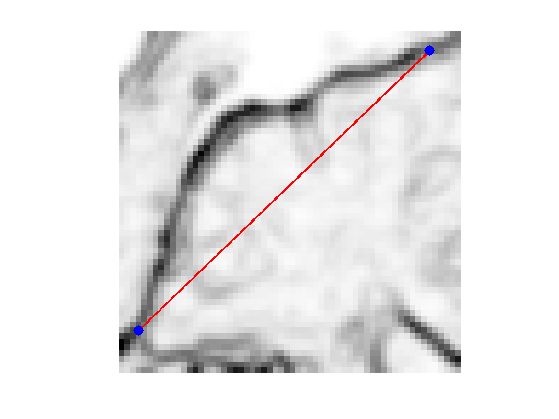
Start and end points \(x_0\) and \(x_1\).

x0 = 4 + 55i;
x1 = 53 + 4i;

Initial curve \(\ga_0\).

p = 128;
t = linspace(0,1,p)';
gamma0 = t*x1 + (1-t)*x0;

Initialize the evolution.

gamma = gamma0;

Display.

clf; hold on;
imageplot(W);
h = plot(imag(gamma([1:end])),real(gamma([1:end])), 'r'); set(h, 'LineWidth', 2);
h = plot(imag(gamma([1 end])),real(gamma([1 end])), 'b.'); set(h, 'MarkerSize', 30);
axis('ij');

Re-sampling for non-periodic curves.

curvabs = @(gamma)[0;cumsum( 1e-5 + abs(gamma(1:end-1)-gamma(2:end)) )];
resample1 = @(gamma,d)interp1(d/d(end),gamma,(0:p-1)'/(p-1), 'linear');
resample = @(gamma)resample1( gamma, curvabs(gamma) );

Time step.

dt = 1/10;

Number of iterations.

Tmax = 2000*4/7;
niter = round(Tmax/dt);

Exercice 6: (check the solution) Perform the curve evolution. Be careful to impose the boundary conditions at each step. 

exo6;


Copyright (c) 2010 Gabriel Peyre