\[ \newcommand{\NN}{\mathbb{N}} \newcommand{\CC}{\mathbb{C}} \newcommand{\GG}{\mathbb{G}} \newcommand{\LL}{\mathbb{L}} \newcommand{\PP}{\mathbb{P}} \newcommand{\QQ}{\mathbb{Q}} \newcommand{\RR}{\mathbb{R}} \newcommand{\VV}{\mathbb{V}} \newcommand{\ZZ}{\mathbb{Z}} \newcommand{\FF}{\mathbb{F}} \newcommand{\KK}{\mathbb{K}} \newcommand{\UU}{\mathbb{U}} \newcommand{\EE}{\mathbb{E}} \newcommand{\Aa}{\mathcal{A}} \newcommand{\Bb}{\mathcal{B}} \newcommand{\Cc}{\mathcal{C}} \newcommand{\Dd}{\mathcal{D}} \newcommand{\Ee}{\mathcal{E}} \newcommand{\Ff}{\mathcal{F}} \newcommand{\Gg}{\mathcal{G}} \newcommand{\Hh}{\mathcal{H}} \newcommand{\Ii}{\mathcal{I}} \newcommand{\Jj}{\mathcal{J}} \newcommand{\Kk}{\mathcal{K}} \newcommand{\Ll}{\mathcal{L}} \newcommand{\Mm}{\mathcal{M}} \newcommand{\Nn}{\mathcal{N}} \newcommand{\Oo}{\mathcal{O}} \newcommand{\Pp}{\mathcal{P}} \newcommand{\Qq}{\mathcal{Q}} \newcommand{\Rr}{\mathcal{R}} \newcommand{\Ss}{\mathcal{S}} \newcommand{\Tt}{\mathcal{T}} \newcommand{\Uu}{\mathcal{U}} \newcommand{\Vv}{\mathcal{V}} \newcommand{\Ww}{\mathcal{W}} \newcommand{\Xx}{\mathcal{X}} \newcommand{\Yy}{\mathcal{Y}} \newcommand{\Zz}{\mathcal{Z}} \newcommand{\al}{\alpha} \newcommand{\la}{\lambda} \newcommand{\ga}{\gamma} \newcommand{\Ga}{\Gamma} \newcommand{\La}{\Lambda} \newcommand{\Si}{\Sigma} \newcommand{\si}{\sigma} \newcommand{\be}{\beta} \newcommand{\de}{\delta} \newcommand{\De}{\Delta} \renewcommand{\phi}{\varphi} \renewcommand{\th}{\theta} \newcommand{\om}{\omega} \newcommand{\Om}{\Omega} \renewcommand{\epsilon}{\varepsilon} \newcommand{\Calpha}{\mathrm{C}^\al} \newcommand{\Cbeta}{\mathrm{C}^\be} \newcommand{\Cal}{\text{C}^\al} \newcommand{\Cdeux}{\text{C}^{2}} \newcommand{\Cun}{\text{C}^{1}} \newcommand{\Calt}[1]{\text{C}^{#1}} \newcommand{\lun}{\ell^1} \newcommand{\ldeux}{\ell^2} \newcommand{\linf}{\ell^\infty} \newcommand{\ldeuxj}{{\ldeux_j}} \newcommand{\Lun}{\text{\upshape L}^1} \newcommand{\Ldeux}{\text{\upshape L}^2} \newcommand{\Lp}{\text{\upshape L}^p} \newcommand{\Lq}{\text{\upshape L}^q} \newcommand{\Linf}{\text{\upshape L}^\infty} \newcommand{\lzero}{\ell^0} \newcommand{\lp}{\ell^p} \renewcommand{\d}{\ins{d}} \newcommand{\Grad}{\text{Grad}} \newcommand{\grad}{\text{grad}} \renewcommand{\div}{\text{div}} \newcommand{\diag}{\text{diag}} \newcommand{\pd}[2]{ \frac{ \partial #1}{\partial #2} } \newcommand{\pdd}[2]{ \frac{ \partial^2 #1}{\partial #2^2} } \newcommand{\dotp}[2]{\langle #1,\,#2\rangle} \newcommand{\norm}[1]{|\!| #1 |\!|} \newcommand{\normi}[1]{\norm{#1}_{\infty}} \newcommand{\normu}[1]{\norm{#1}_{1}} \newcommand{\normz}[1]{\norm{#1}_{0}} \newcommand{\abs}[1]{\vert #1 \vert} \newcommand{\argmin}{\text{argmin}} \newcommand{\argmax}{\text{argmax}} \newcommand{\uargmin}[1]{\underset{#1}{\argmin}\;} \newcommand{\uargmax}[1]{\underset{#1}{\argmax}\;} \newcommand{\umin}[1]{\underset{#1}{\min}\;} \newcommand{\umax}[1]{\underset{#1}{\max}\;} \newcommand{\pa}[1]{\left( #1 \right)} \newcommand{\choice}[1]{ \left\{ \begin{array}{l} #1 \end{array} \right. } \newcommand{\enscond}[2]{ \left\{ #1 \;:\; #2 \right\} } \newcommand{\qandq}{ \quad \text{and} \quad } \newcommand{\qqandqq}{ \qquad \text{and} \qquad } \newcommand{\qifq}{ \quad \text{if} \quad } \newcommand{\qqifqq}{ \qquad \text{if} \qquad } \newcommand{\qwhereq}{ \quad \text{where} \quad } \newcommand{\qqwhereqq}{ \qquad \text{where} \qquad } \newcommand{\qwithq}{ \quad \text{with} \quad } \newcommand{\qqwithqq}{ \qquad \text{with} \qquad } \newcommand{\qforq}{ \quad \text{for} \quad } \newcommand{\qqforqq}{ \qquad \text{for} \qquad } \newcommand{\qqsinceqq}{ \qquad \text{since} \qquad } \newcommand{\qsinceq}{ \quad \text{since} \quad } \newcommand{\qarrq}{\quad\Longrightarrow\quad} \newcommand{\qqarrqq}{\quad\Longrightarrow\quad} \newcommand{\qiffq}{\quad\Longleftrightarrow\quad} \newcommand{\qqiffqq}{\qquad\Longleftrightarrow\qquad} \newcommand{\qsubjq}{ \quad \text{subject to} \quad } \newcommand{\qqsubjqq}{ \qquad \text{subject to} \qquad } \]

Optimal Transport in 1-D

Optimal Transport in 1-D

This tour details the computation of discrete 1-D optimal transport with application to grayscale image histogram manipulations.

Contents

Installing toolboxes and setting up the path.

You need to download the following files: signal toolbox and general toolbox.

You need to unzip these toolboxes in your working directory, so that you have toolbox_signal and toolbox_general in your directory.

For Scilab user: you must replace the Matlab comment '%' by its Scilab counterpart '//'.

Recommandation: You should create a text file named for instance numericaltour.sce (in Scilab) or numericaltour.m (in Matlab) to write all the Scilab/Matlab command you want to execute. Then, simply run exec('numericaltour.sce'); (in Scilab) or numericaltour; (in Matlab) to run the commands.

Execute this line only if you are using Matlab.

getd = @(p)path(p,path); % scilab users must *not* execute this

Then you can add the toolboxes to the path.

getd('toolbox_signal/');
getd('toolbox_general/');

Optimal Transport and Assignement

We consider data \(f \in \RR^{N \times d}\), that can corresponds for instance to an image of \(N\) pixels, with \(d=1\) for grayscale image and \(d=3\) for color image. We denote \(f = (f_i)_{i=1}^N\) with \(f_i \in \RR^d\) the elements of the data.

The discrete (empirical) distribution in \(\RR^d\) associated to this data \(f\) is the sum of Diracs \[ \mu_f = \frac{1}{N} \sum_{i=1}^N \de_{f_i}. \]

An optimal assignement between two such vectors \(f,g \in \RR^{N \times d}\) is a permutation \(\si \in \Si_N\) that minimizes \[ \si^\star \in \uargmin{\si \in \Si_N} \sum_{i=1}^N C(f_i,g_{\si(i)}) \] where \(C(u,v) \in \RR\) is some cost function.

In the following, we consider \(L^p\) costs \[ \forall (u,v) \in \RR^d \times \RR^d, \quad C(u,v) = \norm{u-v}^p \] where \(\norm{\cdot}\) is the Euclidean norm and \(p\geq 1\).

This optimal assignement defines the \(L^p\) Wasserstein distance between the associated point clouds distributions \[ W_p(\mu_f,\mu_g)^p = \sum_{i=1}^N \norm{f_i - g_{\si(i)}}^p = \norm{f - g \circ \si}_p^p \] where \( g \circ \si = (g_{\si(i)})_i \) is the re-ordered points cloud.

Grayscale Image Distribution

We consider here the case \(d=1\), in which case one can compute easily the optimal assignement \(\si^\star\).

Load an image \(f \in \RR^N\) of \(N=n \times n\) pixels.

n = 256;
f = rescale( load_image('lena', n) );

Display it.

clf;
imageplot(f);

A convenient way to visualize the distribution \(\mu_f\) is by computing an histogram \( h \in \RR^Q \) composed using \(Q\) bins \( [u_k,u_{k+1}) \). The histogram is computed as \[ \forall k=1,\ldots,Q, \quad h(p) = \abs{\enscond{i}{ f_i \in [u_k,u_{k+1}) }}. \]

Number of bins.

Q = 50;

Compute the histogram.

[h,t] = hist(f(:), Q);

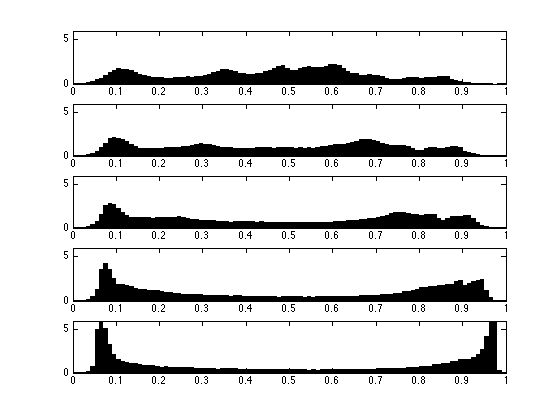
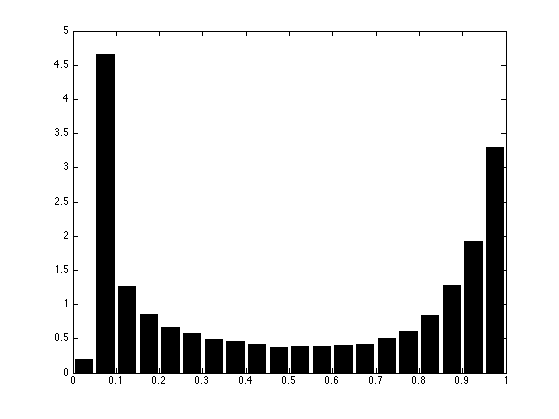
Display this normalized histogram. To make this curve an approximation of a continuous distribution, we normalize \(h\) by \(Q/N\). 

clf;
bar(t,h*Q/n^2); axis('tight');

Exercice 1: (check the solution) Compute and display the histogram of \(f\) for an increasing number of bins. 

exo1;

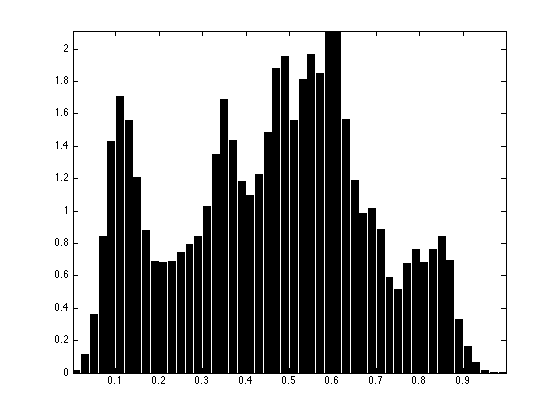
Load another image \(g \in \RR^N\).

g = rescale( mean(load_image('fingerprint', n),3) );

Display it.

clf;
imageplot(g);

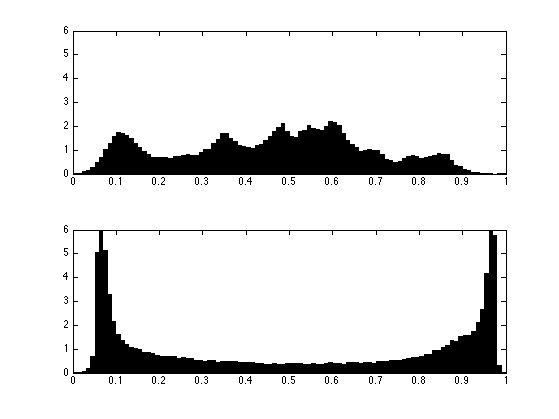
Exercice 2: (check the solution) Compare the two histograms. 

exo2;

1-D Optimal Assignement

For 1-D data, \(d=1\), one can compute explicitely an optimal assignement \(\si^\star \in \Si_N\) for any cost \(C(u,v) = \phi(\abs{u-v})\) where \(\phi : \RR \rightarrow \RR\) is a convex function. This is thus the case for the \(L^p\) optimal transport.

This is obtained by computing two permutations \( \si_f, \si_g \in \Si_N \) that order the values of the data \[ f_{\si_f(1)} \leq f_{\si_f(2)} \leq \ldots f_{\si_f(N)} \] \[ g_{\si_g(1)} \leq g_{\si_g(2)} \leq \ldots g_{\si_g(N)}. \]

An optimal assignement is then optained by assigning, for each \(k\), the index \( i = \si_f(k) \) to the index \( \si_g(k) \), i.e. \[ \si^\star = \si_g \circ \si_f^{-1}\] where \( \si_f^{-1} \) is the inverse permutation, that satisfies \[ \si_f^{-1} \circ \si_f = \text{Id} \].

Note that this optimal assignement \(\si^\star\) is not unique when there are two pixels in \(f\) or \(g\) having the same value.

Compute \(\si_f, \si_g\) in \(O(N \log(N))\) operations using a fast sorting algorithm (e.g. QuickSort).

[~,sigmaf] = sort(f(:));
[~,sigmag] = sort(g(:));

Compute the inverse permutation \(\sigma_f^{-1}\).

sigmafi = [];
sigmafi(sigmaf) = 1:n^2;

Compute the optimal permutation \(\sigma^\star\).

sigma = sigmag(sigmafi);

The optimal assignement is used to compute the projection on the set of image having the pixel distribution \(\mu_g\) \[ \Hh_g = \enscond{m \in \RR^N}{ \mu_m = \mu_g }. \] Indeed, for any \( p > 1 \), the \( L^p \) projector on this set \[ \pi_g( f ) = \uargmin{m \in \Hh_g} \norm{ f - m }_p \] is simply obtained by re-ordering the pixels of \(g\) using an optimal assignement \(\si^\star \in \Si_N\) between \(f\) and \(g\), i.e. \[ \pi_g( f ) = g \circ \si^\star. \]

This projection \(\pi_g( f )\) is called the histogram equalization of \(f\) using the histogram of \(g\)

Compute the projection.

f1 = reshape(g(sigma), [n n]);

Check the new histogram.

clf;
[h,t] = hist(f1(:), p);
bar(t,h*p/n^2);

Compare before/after equalization.

clf;
imageplot(f, 'f', 1,2,1);
imageplot(f1, '\pi_g(f)',  1,2,2);

Histogram Interpolation

We now introduce the linearly interpolated image \[ \forall t \in [0,1], \quad f_t = (1-t) f + t g \circ \sigma^{\star} .\]

One can show that the distribution \( \mu_{f_t} \) is the geodesic interpolation in the \(L^2\)-Wasserstein space between the two distribution \(\mu_f\) (obtained for \(t=0\)) and \(\mu_g\) (obtained for \(t=1\)).

One can also show that it is the barycenter between the two distributions since it has the following variational characterization \[ \mu_{f_t} = \uargmin{\mu} (1-t)W_2(\mu_f,\mu)^2 + t W_2(\mu_g,\mu)^2 . \]

Define the interpolation operator.

ft = @(t)reshape( t*f1 + (1-t)*f, [n n]);

The midway equalization is obtained for \(t=1/2\).

clf;
imageplot(ft(1/2));

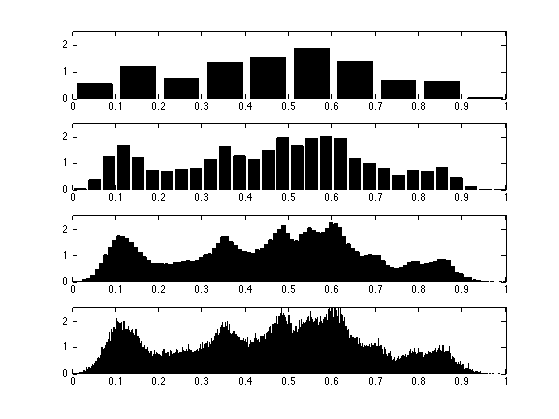
Exercice 3: (check the solution) Display the progression of the interpolation of the histograms. 

exo3;


Copyright (c) 2010 Gabriel Peyre