\[ \newcommand{\NN}{\mathbb{N}} \newcommand{\CC}{\mathbb{C}} \newcommand{\GG}{\mathbb{G}} \newcommand{\LL}{\mathbb{L}} \newcommand{\PP}{\mathbb{P}} \newcommand{\QQ}{\mathbb{Q}} \newcommand{\RR}{\mathbb{R}} \newcommand{\VV}{\mathbb{V}} \newcommand{\ZZ}{\mathbb{Z}} \newcommand{\FF}{\mathbb{F}} \newcommand{\KK}{\mathbb{K}} \newcommand{\UU}{\mathbb{U}} \newcommand{\EE}{\mathbb{E}} \newcommand{\Aa}{\mathcal{A}} \newcommand{\Bb}{\mathcal{B}} \newcommand{\Cc}{\mathcal{C}} \newcommand{\Dd}{\mathcal{D}} \newcommand{\Ee}{\mathcal{E}} \newcommand{\Ff}{\mathcal{F}} \newcommand{\Gg}{\mathcal{G}} \newcommand{\Hh}{\mathcal{H}} \newcommand{\Ii}{\mathcal{I}} \newcommand{\Jj}{\mathcal{J}} \newcommand{\Kk}{\mathcal{K}} \newcommand{\Ll}{\mathcal{L}} \newcommand{\Mm}{\mathcal{M}} \newcommand{\Nn}{\mathcal{N}} \newcommand{\Oo}{\mathcal{O}} \newcommand{\Pp}{\mathcal{P}} \newcommand{\Qq}{\mathcal{Q}} \newcommand{\Rr}{\mathcal{R}} \newcommand{\Ss}{\mathcal{S}} \newcommand{\Tt}{\mathcal{T}} \newcommand{\Uu}{\mathcal{U}} \newcommand{\Vv}{\mathcal{V}} \newcommand{\Ww}{\mathcal{W}} \newcommand{\Xx}{\mathcal{X}} \newcommand{\Yy}{\mathcal{Y}} \newcommand{\Zz}{\mathcal{Z}} \newcommand{\al}{\alpha} \newcommand{\la}{\lambda} \newcommand{\ga}{\gamma} \newcommand{\Ga}{\Gamma} \newcommand{\La}{\Lambda} \newcommand{\Si}{\Sigma} \newcommand{\si}{\sigma} \newcommand{\be}{\beta} \newcommand{\de}{\delta} \newcommand{\De}{\Delta} \renewcommand{\phi}{\varphi} \renewcommand{\th}{\theta} \newcommand{\om}{\omega} \newcommand{\Om}{\Omega} \renewcommand{\epsilon}{\varepsilon} \newcommand{\Calpha}{\mathrm{C}^\al} \newcommand{\Cbeta}{\mathrm{C}^\be} \newcommand{\Cal}{\text{C}^\al} \newcommand{\Cdeux}{\text{C}^{2}} \newcommand{\Cun}{\text{C}^{1}} \newcommand{\Calt}[1]{\text{C}^{#1}} \newcommand{\lun}{\ell^1} \newcommand{\ldeux}{\ell^2} \newcommand{\linf}{\ell^\infty} \newcommand{\ldeuxj}{{\ldeux_j}} \newcommand{\Lun}{\text{\upshape L}^1} \newcommand{\Ldeux}{\text{\upshape L}^2} \newcommand{\Lp}{\text{\upshape L}^p} \newcommand{\Lq}{\text{\upshape L}^q} \newcommand{\Linf}{\text{\upshape L}^\infty} \newcommand{\lzero}{\ell^0} \newcommand{\lp}{\ell^p} \renewcommand{\d}{\ins{d}} \newcommand{\Grad}{\text{Grad}} \newcommand{\grad}{\text{grad}} \renewcommand{\div}{\text{div}} \newcommand{\diag}{\text{diag}} \newcommand{\pd}[2]{ \frac{ \partial #1}{\partial #2} } \newcommand{\pdd}[2]{ \frac{ \partial^2 #1}{\partial #2^2} } \newcommand{\dotp}[2]{\langle #1,\,#2\rangle} \newcommand{\norm}[1]{|\!| #1 |\!|} \newcommand{\normi}[1]{\norm{#1}_{\infty}} \newcommand{\normu}[1]{\norm{#1}_{1}} \newcommand{\normz}[1]{\norm{#1}_{0}} \newcommand{\abs}[1]{\vert #1 \vert} \newcommand{\argmin}{\text{argmin}} \newcommand{\argmax}{\text{argmax}} \newcommand{\uargmin}[1]{\underset{#1}{\argmin}\;} \newcommand{\uargmax}[1]{\underset{#1}{\argmax}\;} \newcommand{\umin}[1]{\underset{#1}{\min}\;} \newcommand{\umax}[1]{\underset{#1}{\max}\;} \newcommand{\pa}[1]{\left( #1 \right)} \newcommand{\choice}[1]{ \left\{ \begin{array}{l} #1 \end{array} \right. } \newcommand{\enscond}[2]{ \left\{ #1 \;:\; #2 \right\} } \newcommand{\qandq}{ \quad \text{and} \quad } \newcommand{\qqandqq}{ \qquad \text{and} \qquad } \newcommand{\qifq}{ \quad \text{if} \quad } \newcommand{\qqifqq}{ \qquad \text{if} \qquad } \newcommand{\qwhereq}{ \quad \text{where} \quad } \newcommand{\qqwhereqq}{ \qquad \text{where} \qquad } \newcommand{\qwithq}{ \quad \text{with} \quad } \newcommand{\qqwithqq}{ \qquad \text{with} \qquad } \newcommand{\qforq}{ \quad \text{for} \quad } \newcommand{\qqforqq}{ \qquad \text{for} \qquad } \newcommand{\qqsinceqq}{ \qquad \text{since} \qquad } \newcommand{\qsinceq}{ \quad \text{since} \quad } \newcommand{\qarrq}{\quad\Longrightarrow\quad} \newcommand{\qqarrqq}{\quad\Longrightarrow\quad} \newcommand{\qiffq}{\quad\Longleftrightarrow\quad} \newcommand{\qqiffqq}{\qquad\Longleftrightarrow\qquad} \newcommand{\qsubjq}{ \quad \text{subject to} \quad } \newcommand{\qqsubjqq}{ \qquad \text{subject to} \qquad } \]

Subdivision Curves

Subdivision Curves

Subdvision methods progressively refine a discrete curve and converge to a smooth curve. This allows to perform an interpolation or approximation of a given coarse dataset.

Contents

Installing toolboxes and setting up the path.

You need to download the following files: signal toolbox, general toolbox, graph toolbox and wavelet_meshes toolbox.

You need to unzip these toolboxes in your working directory, so that you have toolbox_signal, toolbox_general, toolbox_graph and toolbox_wavelet_meshes in your directory.

For Scilab user: you must replace the Matlab comment '%' by its Scilab counterpart '//'.

Recommandation: You should create a text file named for instance numericaltour.sce (in Scilab) or numericaltour.m (in Matlab) to write all the Scilab/Matlab command you want to execute. Then, simply run exec('numericaltour.sce'); (in Scilab) or numericaltour; (in Matlab) to run the commands.

Execute this line only if you are using Matlab.

getd = @(p)path(p,path); % scilab users must *not* execute this

Then you can add the toolboxes to the path.

getd('toolbox_signal/');
getd('toolbox_general/');
getd('toolbox_graph/');
getd('toolbox_wavelet_meshes/');

Curve Subdivision

Starting from an initial set of control points (which can be seen as a coarse curve), subdivision produces a smooth 2-D curve.

Shortcut to plot a periodic curve.

ms = 20; lw = 1.5;
myplot = @(f,c)plot(f([1:end 1]), c, 'LineWidth', lw, 'MarkerSize', ms);
myaxis = @(rho)axis([-rho 1+rho -rho 1+rho], 'off');

We represent a dicretized curve of \(N\) points as a vector of complex numbers \(f \in \CC^N\). Since we consider periodic boundary conditions, we assume the vectors have periodic boundary conditions.

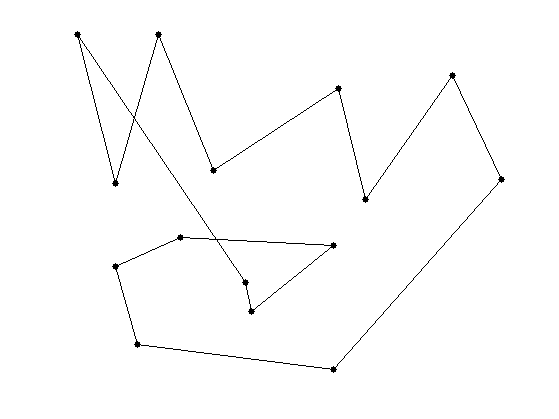
Define the initial coarse set of control points \(f_0 \in \CC^{N_0}\).

f0 =    [0.11 0.18 0.26 0.36 0.59 0.64 0.80 0.89 0.58 0.22 0.18 0.30 0.58 0.43 0.42]' + ...
   1i * [0.91 0.55 0.91 0.58 0.78 0.51 0.81 0.56 0.10 0.16 0.35 0.42 0.40 0.24 0.31]';

Rescale it to fit in a box.

f0 = rescale(real(f0),.01,.99) + 1i * rescale(imag(f0),.01,.99);

Display it.

clf; myplot(f0, 'k.-');
myaxis(0);

One subdivision step reads \[ f_{j+1} = (f_j \uparrow 2) \star h. \] This produces discrete curves \(f_j \in \CC^{N_j}\) where \(N_j = N_0 2^j\).

Here \(\uparrow 2\) is the up-sampling operator \[ (f \uparrow 2)_{2i}=f_i \qandq (f \uparrow 2)_{2i+1} = 0. \]

Recall that the periodic discrete convolution is defined as \[ (f \star h)_i = \sum_j f_j h_{i-j}, \] where the filter \(h\) is zero-padded to reach the same size as \(f\).

The low pass filter (subdivision kernel) \(h \in \CC^K\) should satisfies \[ \sum_i h_i = 2 . \] This ensure that the center of gravity of the curve stays constant \[ \frac{1}{N_j} \sum_{i=1}^{N_j} f_{j,i} = \frac{1}{N_0} \sum_{i=1}^{N_0} f_{0,i}.\]

Define the subdivision operator that maps \(f_j\) to \(f_{j+1}\).

subdivide = @(f,h)cconv( upsampling(f), h);

We use here the kernel \[ h = \frac{1}{8}[1, 4, 6, 4, 1]. \] It produced a cubic B-spline interpolation.

h = [1 4 6 4 1];
h = 2*h/sum(h(:));

Initilize the subdivision with \(f_0\) at scale \(j=0\).

f = f0;

Perform one step.

f = subdivide(f,h);

Display the original and filtered discrete curves.

clf; hold on;
myplot(f, 'k.-');
myplot(f0, 'r.--');
myaxis(0);

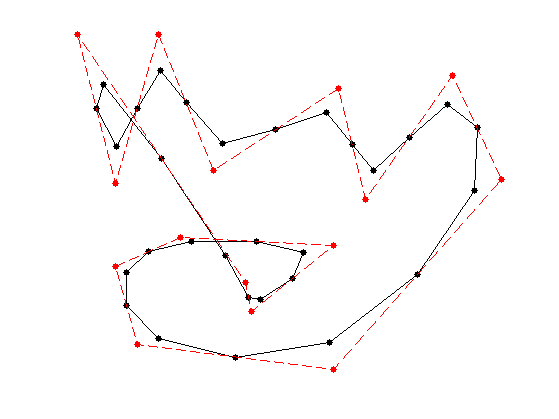
Exercice 1: (check the solution) Perform several step of subdivision. Display the different curves. 

exo1;

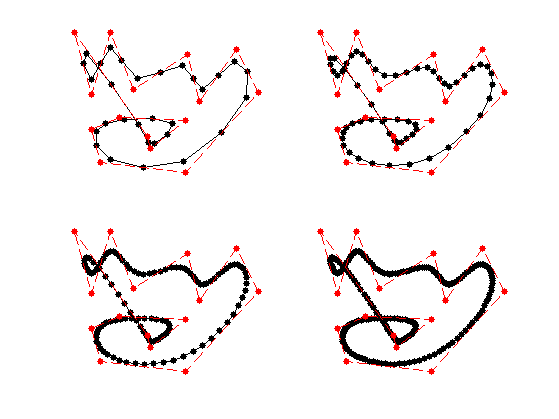
Under some restriction on the kernel \(h\), one can show that these discrete curves converges (e.g. in Hausdorff distance) toward a smooth limit curve \(f^\star : [0,1] \rightarrow \CC\).

We do not details here sufficient condition to ensure convergence and smoothness of the limitting curve. The interested reader can have a look at [DynLevin02] for a review of theoritical guarantees for subdivision.

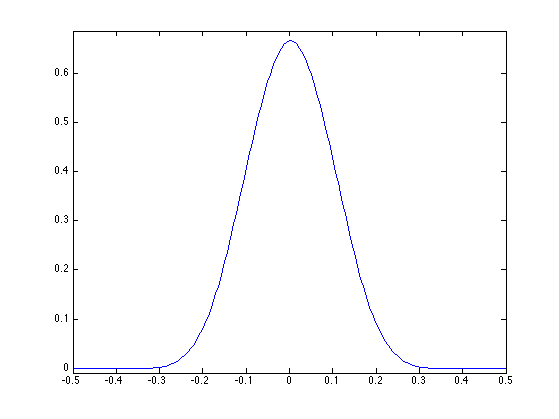
The limit curve \(f^\star\) is a weighted average of the initial points \(f_0 = (f_{0,i})_{i=0}^{N_0-1} \in \CC^{N_0}\) using a continuous scaling function \(\phi : [0,1] \rightarrow \RR\) \[ f^\star(t) = \sum_{i=0}^{N_0-1} f_{0,i} \phi(t-i/N_0). \] The continuous kernel \(\phi\) is a low-pass function which as a compact support of width \(K/N_0\). The control point \(f_{0,i}\) thus only influences the final curve \(f^\star\) around \(t=i/N_0\).

The scaling function \(\phi\) can be computed as the limit of the sub-division process \(f_j\) when starting from \(f_0 = \delta = [1,0,\ldots,0]\), which is the Dirac vector.

Exercice 2: (check the solution) Compute the scaling function \(\phi\) associated to the subdivision. 

exo2;

Exercice 3: (check the solution) Test with different configurations of control points. 

exo3;

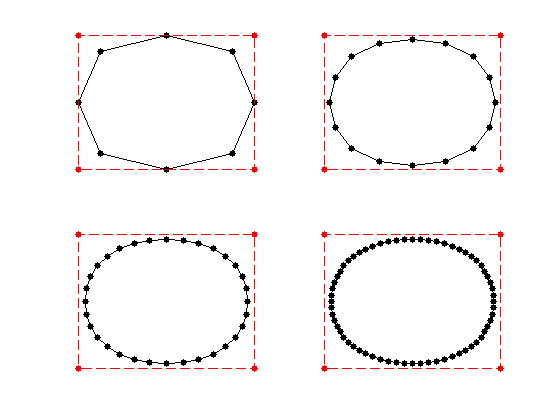
Quadratic B-splines

We consider here the Chaikin "corner cutting" scheme [Chaikin74].

For a weight \(w>1\), it corresponds to the following kernel: \[ h = \frac{1}{1+w}[1, w, w, 1]. \] The weight is a tension parameter that controls the properties of the interpolation. 

hcc = @(w)[1 w w 1]/(1+w);

For \(w=3\), the scaling function \(\phi\) is a quadratic B-spline.

Exercice 4: (check the solution) Test the corner-cutting for \(w=3\). 

exo4;

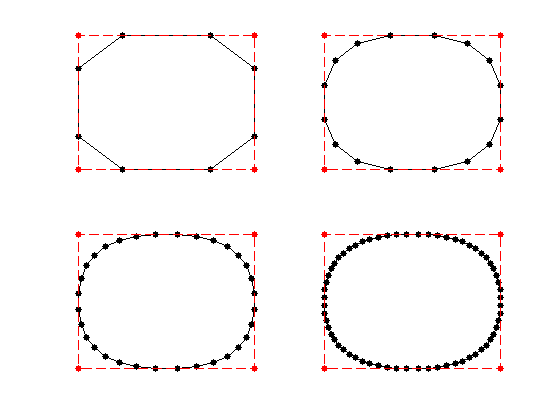
Exercice 5: (check the solution) Test the corner-cutting for vaious values of \(w\). 

exo5;

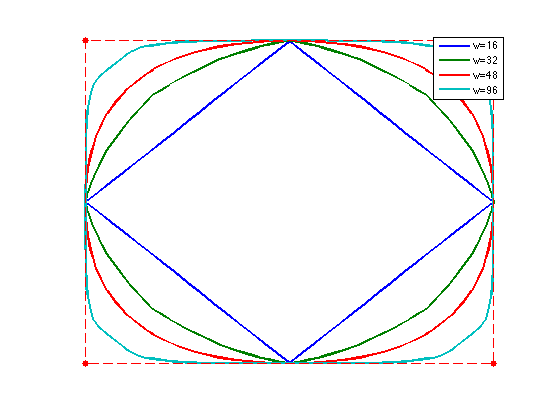
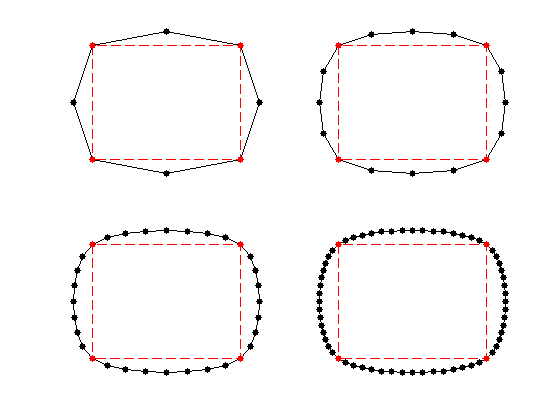
Interpolating Subdivision

Interpolating schemes keeps unchange the set of point at the previous level, and only smooth the position of the added points.

A subdivision is interpolating if the kernel satisfies \[ h(0)=1 \qandq \forall i \neq 0, \quad h(2i)=0. \]

We consider the four-point interpolation kernel proposed in [DynLevGre87]: \[ h = [-w, 0, 1/2+w, 1, 1/2+w, -w] \] where \(w>0\) is a tension parameter. 

h4pt = @(w)[-w, 0, 1/2+w, 1, 1/2+w, 0, -w];

One usually choose \(w=1/16\) wich corresponds to cubic B-spline interpolation. It can be shown to produce \(C^1\) curves for \( w \in [0, (\sqrt{5}-1)/8 \approx 0.154] \), see [DynGreLev91].

Exercice 6: (check the solution) Perform the interpolating subdivision for \(w=1/16\). 

exo6;

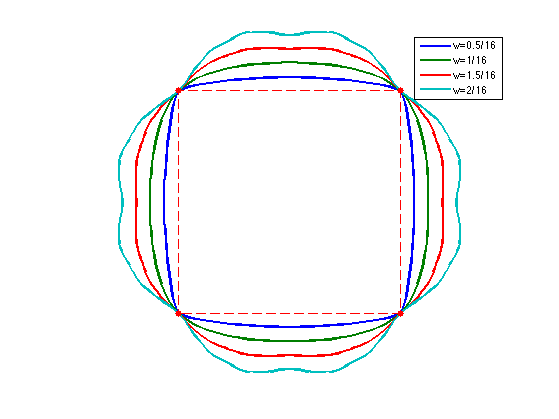
Exercice 7: (check the solution) Test the influence of \(w\). 

exo7;

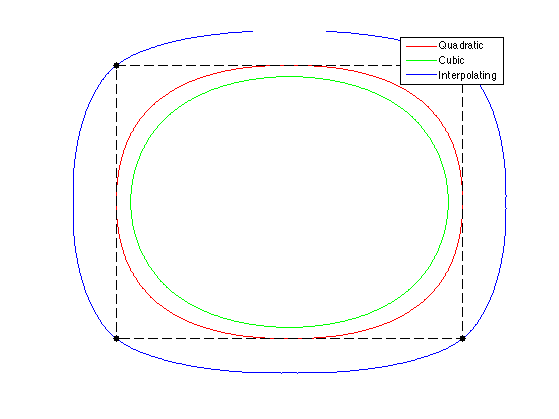
Exercice 8: (check the solution) Compare the result of the quadratic B-spline, cubic B-spline, and 4-points interpolating. 

exo8;

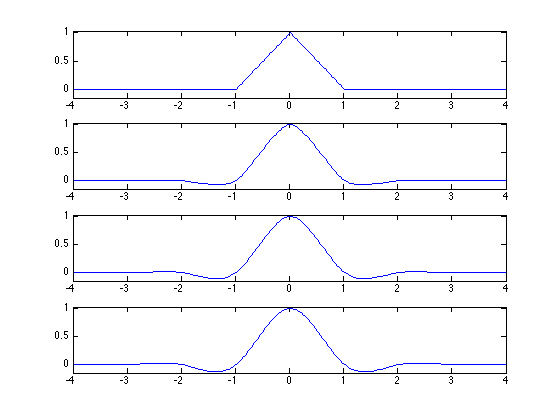
The 4-point scheme for \(w=1/16\) is generalized to \(2k\)-point schemes of Deslauriers-Dubuc [DeslDub89]. This corresponds to computing a polynomial interpolation of degree \(2k-1\), which generalizes the cubic interpolation. Using larger \(k\) leads to smoother interpolation, at the price of a larger interpolation kernel.

We give here the odd coefficients of the filters.

H = {   [0.5000 0.5000], ...
        [-0.0625, 0.5625, 0.5625, -0.0625], ...
        [0.0117, -0.0977, 0.5859, 0.5859, -0.0977, 0.0117], ...
        [-0.0024, 0.0239, -0.1196, 0.5981, 0.5981, -0.1196, 0.0239, -0.0024] };
hdd = @(k)assign(assign(zeros(4*k-1,1),1:2:4*k-1,H{k}), 2*k, 1);

Exercice 9: (check the solution) Display the scaling function associated to these Deslauriers-Dubuc filters. 

exo9;

Curve Approximation

Given an input, complicated curve \(g : [0,1] \rightarrow \CC\), it is possible to approximate is by sampling the curve, and then subdividing it. It corresponds to a low pass filtering approximation.

Load an initial random curve, which is a high resolution curve \(g\).

options.bound = 'per';
n = 1024*2;
sigma = n/8;
F = perform_blurring(randn(n,1),sigma,options) + 1i*perform_blurring(randn(n,1),sigma,options);
F = rescale(real(F),.01,.99) + 1i * rescale(imag(F),.01,.99);

Display it.

clf; myplot(F, 'k');
myaxis(0);

Load an interpolating subvision mask.

h = [-1, 0, 9, 1, 9, 0, -1]/16;
h((end+1)/2)=1;

Exercice 10: (check the solution) Perform an approximation \(f\) of the curve using a uniform sampling with \(N_0=20\) points. 

exo10;

To quantify the quality of the approximation, we use an averaged Hausdorff distance. The distance between two sets of points \(X\) and \(Y\) is \[ d(X,Y) = d_0(X,Y)+d_0(Y,X) \qwhereq d_0(X,Y)^2 = \frac{1}{\abs{X}} \sum_{x \in X} \umin{y \in Y} \norm{x-y}^2. \]

Compute the pairwise distances matrix \(D_{i,j} = \norm{f_i-g_j}^2\) between points.

dist = @(f,g)abs( repmat(f, [1 length(g)]) - repmat(transpose(g), [length(f) 1]) );

Compute the Hausdorff distance.

hausdorff = @(f,g)sqrt( mean(min(dist(f,g)).^2) );
hausdorff = @(f,g)hausdorff(f,g) + hausdorff(g,f);

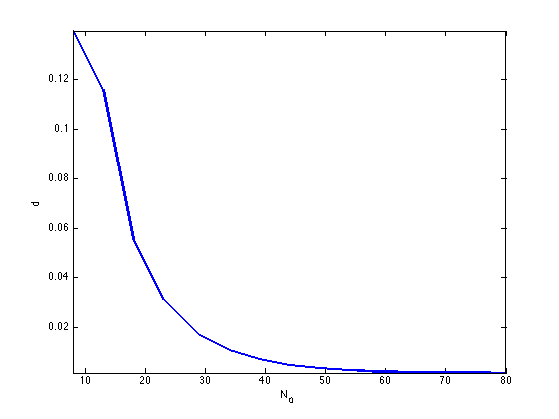
Exercice 11: (check the solution) Display the decay of the Hausdorff approximation error as the number \(N_0\) of sampling points increases. 

exo11;

3-D Curve Subdivision

It is possible to construct 3-D curves by subdivision.

Exercice 12: (check the solution) Perform curve subdivision in 3D space. 

exo12;

Bibliography


Copyright (c) 2010 Gabriel Peyre