\[ \newcommand{\NN}{\mathbb{N}} \newcommand{\CC}{\mathbb{C}} \newcommand{\GG}{\mathbb{G}} \newcommand{\LL}{\mathbb{L}} \newcommand{\PP}{\mathbb{P}} \newcommand{\QQ}{\mathbb{Q}} \newcommand{\RR}{\mathbb{R}} \newcommand{\VV}{\mathbb{V}} \newcommand{\ZZ}{\mathbb{Z}} \newcommand{\FF}{\mathbb{F}} \newcommand{\KK}{\mathbb{K}} \newcommand{\UU}{\mathbb{U}} \newcommand{\EE}{\mathbb{E}} \newcommand{\Aa}{\mathcal{A}} \newcommand{\Bb}{\mathcal{B}} \newcommand{\Cc}{\mathcal{C}} \newcommand{\Dd}{\mathcal{D}} \newcommand{\Ee}{\mathcal{E}} \newcommand{\Ff}{\mathcal{F}} \newcommand{\Gg}{\mathcal{G}} \newcommand{\Hh}{\mathcal{H}} \newcommand{\Ii}{\mathcal{I}} \newcommand{\Jj}{\mathcal{J}} \newcommand{\Kk}{\mathcal{K}} \newcommand{\Ll}{\mathcal{L}} \newcommand{\Mm}{\mathcal{M}} \newcommand{\Nn}{\mathcal{N}} \newcommand{\Oo}{\mathcal{O}} \newcommand{\Pp}{\mathcal{P}} \newcommand{\Qq}{\mathcal{Q}} \newcommand{\Rr}{\mathcal{R}} \newcommand{\Ss}{\mathcal{S}} \newcommand{\Tt}{\mathcal{T}} \newcommand{\Uu}{\mathcal{U}} \newcommand{\Vv}{\mathcal{V}} \newcommand{\Ww}{\mathcal{W}} \newcommand{\Xx}{\mathcal{X}} \newcommand{\Yy}{\mathcal{Y}} \newcommand{\Zz}{\mathcal{Z}} \newcommand{\al}{\alpha} \newcommand{\la}{\lambda} \newcommand{\ga}{\gamma} \newcommand{\Ga}{\Gamma} \newcommand{\La}{\Lambda} \newcommand{\Si}{\Sigma} \newcommand{\si}{\sigma} \newcommand{\be}{\beta} \newcommand{\de}{\delta} \newcommand{\De}{\Delta} \renewcommand{\phi}{\varphi} \renewcommand{\th}{\theta} \newcommand{\om}{\omega} \newcommand{\Om}{\Omega} \renewcommand{\epsilon}{\varepsilon} \newcommand{\Calpha}{\mathrm{C}^\al} \newcommand{\Cbeta}{\mathrm{C}^\be} \newcommand{\Cal}{\text{C}^\al} \newcommand{\Cdeux}{\text{C}^{2}} \newcommand{\Cun}{\text{C}^{1}} \newcommand{\Calt}[1]{\text{C}^{#1}} \newcommand{\lun}{\ell^1} \newcommand{\ldeux}{\ell^2} \newcommand{\linf}{\ell^\infty} \newcommand{\ldeuxj}{{\ldeux_j}} \newcommand{\Lun}{\text{\upshape L}^1} \newcommand{\Ldeux}{\text{\upshape L}^2} \newcommand{\Lp}{\text{\upshape L}^p} \newcommand{\Lq}{\text{\upshape L}^q} \newcommand{\Linf}{\text{\upshape L}^\infty} \newcommand{\lzero}{\ell^0} \newcommand{\lp}{\ell^p} \renewcommand{\d}{\ins{d}} \newcommand{\Grad}{\text{Grad}} \newcommand{\grad}{\text{grad}} \renewcommand{\div}{\text{div}} \newcommand{\diag}{\text{diag}} \newcommand{\pd}[2]{ \frac{ \partial #1}{\partial #2} } \newcommand{\pdd}[2]{ \frac{ \partial^2 #1}{\partial #2^2} } \newcommand{\dotp}[2]{\langle #1,\,#2\rangle} \newcommand{\norm}[1]{|\!| #1 |\!|} \newcommand{\normi}[1]{\norm{#1}_{\infty}} \newcommand{\normu}[1]{\norm{#1}_{1}} \newcommand{\normz}[1]{\norm{#1}_{0}} \newcommand{\abs}[1]{\vert #1 \vert} \newcommand{\argmin}{\text{argmin}} \newcommand{\argmax}{\text{argmax}} \newcommand{\uargmin}[1]{\underset{#1}{\argmin}\;} \newcommand{\uargmax}[1]{\underset{#1}{\argmax}\;} \newcommand{\umin}[1]{\underset{#1}{\min}\;} \newcommand{\umax}[1]{\underset{#1}{\max}\;} \newcommand{\pa}[1]{\left( #1 \right)} \newcommand{\choice}[1]{ \left\{ \begin{array}{l} #1 \end{array} \right. } \newcommand{\enscond}[2]{ \left\{ #1 \;:\; #2 \right\} } \newcommand{\qandq}{ \quad \text{and} \quad } \newcommand{\qqandqq}{ \qquad \text{and} \qquad } \newcommand{\qifq}{ \quad \text{if} \quad } \newcommand{\qqifqq}{ \qquad \text{if} \qquad } \newcommand{\qwhereq}{ \quad \text{where} \quad } \newcommand{\qqwhereqq}{ \qquad \text{where} \qquad } \newcommand{\qwithq}{ \quad \text{with} \quad } \newcommand{\qqwithqq}{ \qquad \text{with} \qquad } \newcommand{\qforq}{ \quad \text{for} \quad } \newcommand{\qqforqq}{ \qquad \text{for} \qquad } \newcommand{\qqsinceqq}{ \qquad \text{since} \qquad } \newcommand{\qsinceq}{ \quad \text{since} \quad } \newcommand{\qarrq}{\quad\Longrightarrow\quad} \newcommand{\qqarrqq}{\quad\Longrightarrow\quad} \newcommand{\qiffq}{\quad\Longleftrightarrow\quad} \newcommand{\qqiffqq}{\qquad\Longleftrightarrow\qquad} \newcommand{\qsubjq}{ \quad \text{subject to} \quad } \newcommand{\qqsubjqq}{ \qquad \text{subject to} \qquad } \]

Cartoon+Texture Variational Image Decomposition

Cartoon+Texture Variational Image Decomposition

This numerical tour explores the use of variational energies to decompose an image into a cartoon and a texture layer.

Contents

Installing toolboxes and setting up the path.

You need to download the following files: signal toolbox and general toolbox.

You need to unzip these toolboxes in your working directory, so that you have toolbox_signal and toolbox_general in your directory.

For Scilab user: you must replace the Matlab comment '%' by its Scilab counterpart '//'.

Recommandation: You should create a text file named for instance numericaltour.sce (in Scilab) or numericaltour.m (in Matlab) to write all the Scilab/Matlab command you want to execute. Then, simply run exec('numericaltour.sce'); (in Scilab) or numericaltour; (in Matlab) to run the commands.

Execute this line only if you are using Matlab.

getd = @(p)path(p,path); % scilab users must *not* execute this

Then you can add the toolboxes to the path.

getd('toolbox_signal/');
getd('toolbox_general/');

A variational image separation finds a decomposition \(f = u^\star + v^\star + w^\star\) where \(u^\star\) and \(v^\star\) are solutions of an optimization problem of the form \[ \min_{u,v} \: \frac{1}{2}\|f-u-v\|^2 + \lambda J(u) + \mu T(v), \]

where \(J(u)\) is a cartoon image prior (that favors edges) and \(T(v)\) is a texture image prior (that favors oscillations). The parameters \(\lambda,\mu\) should be adapted to the noise level and the amount of edge/textures.

When no noise is present in \(f\), so that \(w^\star=0\), on minimizes \[ \min_{u} \: T(f-u) + \lambda J(u). \]

In this tour, we define \(J\) as the total variation prior. For \(T\), we use the Hilbert norm framework introduced in:

Constrained and SNR-based Solutions for TV-Hilbert Space Image Denoising, Jean-François Aujol and Guy Gilboa, Journal of Mathematical Imaging and Vision, volume 26, numbers 1-2, pages 217-237, November 2006.

Total Variation Cartoon Prior

The total variation is a Banach norm. On the contrary to the Sobolev norm, it is able to take into account step edges.

First we load a textured image.

n = 256;
name = 'boat';
f = rescale( crop(load_image(name),n) );

Display it.

clf;
imageplot(f);

The total variation of a smooth image \(f\) is defined as \[J(f)=\int \|\nabla f(x)\| d x\]

It is extended to non-smooth images having step discontinuities.

The total variation of an image is also equal to the total length of its level sets. \[J(f)=\int_{-\infty}^{+\infty} L( S_t(f) ) dt\]

Where \(S_t(f)\) is the level set at \(t\) of the image \(f\) \[S_t(f)=\{ x \backslash f(x)=t \}\]

The Gradient of the TV norm is \[ \text{Grad}J(f) = \text{div}\left( \frac{\nabla f}{\|\nabla f\|} \right) . \]

The gradient of the TV norm is not defined if at a pixel \(x\) one has \(\nabla f(x)=0\). This means that the TV norm is difficult to minimize, and its gradient flow is not well defined.

To define a gradient flow, we consider instead a smooth TV norm \[J_\epsilon(f) = \int \sqrt{ \varepsilon^2 + \| \nabla f(x) \|^2 } d x\]

This corresponds to replacing \(\|u\|\) by \( \sqrt{\varepsilon^2 + \|u\|^2} \) which is a smooth function.

We display (in 1D) the smoothing of the absolute value.

u = linspace(-5,5)';
clf;
subplot(2,1,1); hold('on');
plot(u, abs(u), 'b');
plot(u, sqrt(.5^2+u.^2), 'r');
title('\epsilon=1/2'); axis('square');
subplot(2,1,2); hold('on');
plot(u, abs(u), 'b');
plot(u, sqrt(1^2+u.^2), 'r');
title('\epsilon=1'); axis('square');

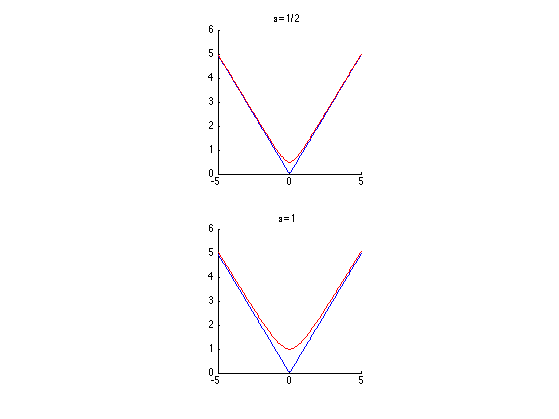
In the following we set a small enough regularization parameter \(\varepsilon\).

epsilon = 1e-2;

Compute the (smoothed) total variation of \(f\).

J = @(u)sum(sum( sqrt( epsilon^2 + sum3(grad(u).^2,3) ) ));
disp(['J(f) = ' num2str(J(f),3)]);

J(f) = 4.37e+03

TV-\(L^2\) Model

The simplest decomposition method performs a total variation denoising: \[\min_u \frac{1}{2}\|f-u\|^2 + \lambda J(u).\]

It corresponds to the TV-\(L^2\) model of Rudin-Osher-Fatermi, because the texture prior is the \(L^2\) norm: \[ T(v) = \frac{1}{2} \|v\|^2. \]

This a poor texture prior because it just assumes the texture has a small overall energy, and does not care about the oscillations.

Define the regularization parameter \(\lambda\).

lambda = .2;

The step size for diffusion should satisfy: \[ \tau < \frac{2}{1 + \lambda 8 / \varepsilon} . \]

tau = 1.9 / ( 1 + lambda * 8 / epsilon);

Initialization of the minimization.

u = f;

The Gradient of the smoothed TV norm is \[ \text{Grad}J(f) = \text{div}\left( \frac{\nabla f}{\sqrt{\varepsilon^2 + \|\nabla f\|^2}} \right) . \]

Shortcut for the gradient of the smoothed TV norm.

GradJ0 = @(Gr)-div( Gr ./ repmat( sqrt( epsilon^2 + sum3(Gr.^2,3) ) , [1 1 2]) );
GradJ = @(u)GradJ0(grad(u));

One step of descent.

u = u - tau*( u - f + lambda* GradJ(u) );

Exercice 1: (check the solution) Compute the gradient descent and monitor the minimized energy. 

exo1;

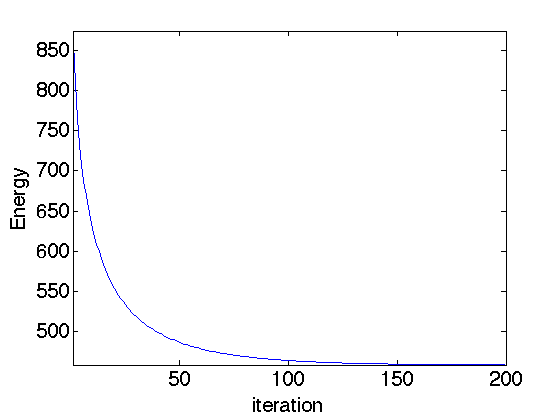
Display the cartoon layer.

clf;
imageplot(u);

Shortcut to increase the contrast of the textured layer for better display.

rho = .8; % constrast factor
eta = .2; % saturation limit
displaytexture0 = @(x)sign(x).*abs(x).^rho;
displaytexture  = @(v)displaytexture0( clamp(v,-eta,eta)/eta );

Display the textured layer.

clf;
imageplot( displaytexture(f-u) );

Gabor Hilbert Energy

To model the texture, one should use a prior \(T(v)\) that favors oscillations. We thus use a weighted \(L^2\) norms computed over the Fourier domain: \[ T(v) = \frac{1}{2} \sum_{\omega} \|W_{\omega} \hat f(\omega) \|^2 \] where \(W_\omega\) is the weight associated to the frequency \(\omega\).

This texture norm can be rewritten using the Fourier transform \(F\) as \[ T(v) = \frac{1}{2} \|\text{diag}(W)F u\|^2 \quad\text{where}\quad (Fu)_\omega = \hat u(\omega).\]

To favor oscillation, we use a weight that is large for low frequency and small for large frequency. A simple Hilbert norm is a inverse Sobolev space \(H^{-1}\).

It was first introduced in:

S.J. Osher, A. Sole, and L.A. Vese, Image decomposition and restoration using total variation minimization and the \(H^{-1}\) norm, SIAM Multiscale Modeling and Simulation, 1(3):349-370, 2003.

This Hilbert norm is defined using \[ W_\omega = \frac{1}{ \| \omega \| + \eta } \] where \(\eta>0\) is a small constant that prevents explosion at low frequencies. 

eta = .05;
x = [0:n/2-1, -n/2:-1]/n;
[Y,X] = meshgrid(x,x);
W = 1 ./ (eta + sqrt(X.^2 + Y.^2));

Display the inverse weight, with 0 frequency in the middle.

imageplot(fftshift(1./W));

Compute the texture norm. The \(1/n\) normalization is intended to make the Fourier transform orthogonal.

T = @(v)1/2*norm( W.*fft2(v)/n, 'fro' ).^2;
disp(['T(f) = ' num2str(T(f), 3) ] );

T(f) = 4.81e+06

The gradient of the texture norm is \[\text{Grad}T(v) = H v \quad\text{where}\quad H = F^* \text{diag}(W^2) F, \] where \(F^*\) is the inverse Fourier transform. Note that if \(\eta=1\), this gradient is the inverse Laplacian \[ \text{Grad}T(v) = \Delta^{-1} v. \]

Define the filtering operator \( \text{Grad}T \).

GradT = @(f)real(ifft2(W.^2.*fft2(f)));

This is a low pass filter.

imageplot(GradT(f));

Define its inverse \( (\text{Grad}T)^{-1} \).

GradTInv = @(f)real(ifft2(fft2(f)./W.^2));

It is a high pass filter.

imageplot(GradTInv(f));

TV-\(H^{-1}\) Image Decomposition

The TV-Hilbert decomposition solves \[ \min_u \mathcal{E}(u) = \frac{1}{2} \| W F(f-u) \|^2 + \lambda J(u). \]

The mapping \(u \mapsto \mathcal{E}(u) \) is a smooth functional, it can thus be minimized using a gradient descent: \[ f^{(\ell+1)} = f^{(\ell)} - \tau \left( H(u-f) + \lambda \text{Grad}J(u) \right). \]

The parameter \(\lambda\) for the texture/cartoon tradeoff.

lambda = 5;

The gradient descent step size should satisfy: \[ \tau < \frac{2}{ \max_{\omega} W_\omega^2 + \lambda \epsilon /8 } \]

tau = 1.9 /( max(W(:))^2 + 8*lambda/epsilon );

Initial cartoon layer.

u = f;

Gradient descent step.

u = u - tau * ( GradT(u-f) + lambda*GradJ(u) );

Exercice 2: (check the solution) Perform the gradient descent, monitor the decay of the energy. 

exo2;

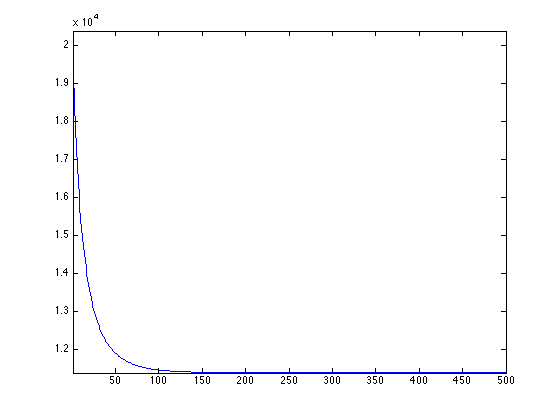
Display the cartoon layer.

clf;
imageplot(u);

Display the textured layer.

clf;
imageplot( displaytexture(f-u) );

TV-Gabor Image Decomposition

The \(H^{-1}\) texture model is intended to capture very high frequency, and thus performs poorly for medium frequency textures.

To capture these patterns, we follow:

Structure-Texture Image Decomposition - Modeling, Algorithms, and Parameter Selection, Jean-Francois Aujol, Guy Gilboa, Tony Chan, and Stanley Osher, International Journal of Computer Vision, volume 67, number 1, pages 111-136, April 2006

and we use a radial weight profile centered around a frequency \(r\).

To determine the target frequency \(r\), we analyse a sub-window around a point \(p\) of the image containing approximately a single frequency.

Location \(p\) of the sub-window.

p = [125 200];

Size \(\mu\), in pixels, of the sub-window.

mu = 10;

Compute a Gaussian mask.

[Y,X] = meshgrid( 1:n, 1:n );
U = exp( ( -(X-p(1)).^2 - (Y-p(2)).^2 )/(2*mu^2)  );

Display the masked image.

clf;
imageplot(U.*f);

Remove the low frequencies from the Fourier transform, after centering.

F = fft2(U.*f);
F = fftshift(F);
F(end/2-20:end/2+20,end/2-20:end/2+20) = 0;

Compute the location \(x_m,y_m\) of the pick of the spectrum.

[tmp,i] = max(abs(F(:)));
[xm,ym] = ind2sub([n n], i);

Display.

clf; hold on;
imageplot(abs(F));
h = plot( [ym n-ym], [xm  n-xm], 'r.' );
set(h, 'MarkerSize', 20);

Target frequency is the distance between \( (x_m,y_m) \) and the center frequency.

r = sqrt( (xm-n/2)^2 + (ym-n/2)^2 );

We use the following weights: \[ W_\omega = 1 - e^{ -\frac{(\|\omega\|-r)^2}{ 2 \sigma^2 } } \] where \( \sigma>0 \) controls the precision one expect about the frequency location.

Radial weight profile.

sigma = 10;
x = [0:n/2-1, -n/2:-1];
[Y,X] = meshgrid(x,x);
R = sqrt(X.^2+Y.^2);
W = 1 - exp( -(r-R).^2 / (2*sigma^2) );

Display the weight.

imageplot(fftshift(W));

Exercice 3: (check the solution) Define the operators \(\text{Grad} T\) and apply it to an images. 

exo3;

Exercice 4: (check the solution) For a well chosen value of \(\lambda\), perform the TV-Hilbert decomposition with this texture kernel. 

exo4;

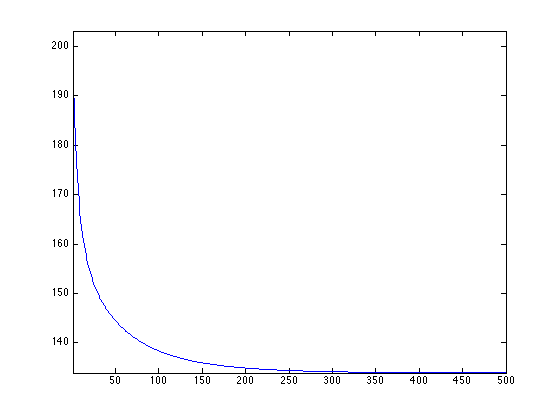
Display the cartoon layer.

clf;
imageplot(u);

Display the textured layer.

clf;
imageplot( displaytexture(f-u) );


Copyright (c) 2010 Gabriel Peyre