\[ \newcommand{\NN}{\mathbb{N}} \newcommand{\CC}{\mathbb{C}} \newcommand{\GG}{\mathbb{G}} \newcommand{\LL}{\mathbb{L}} \newcommand{\PP}{\mathbb{P}} \newcommand{\QQ}{\mathbb{Q}} \newcommand{\RR}{\mathbb{R}} \newcommand{\VV}{\mathbb{V}} \newcommand{\ZZ}{\mathbb{Z}} \newcommand{\FF}{\mathbb{F}} \newcommand{\KK}{\mathbb{K}} \newcommand{\UU}{\mathbb{U}} \newcommand{\EE}{\mathbb{E}} \newcommand{\Aa}{\mathcal{A}} \newcommand{\Bb}{\mathcal{B}} \newcommand{\Cc}{\mathcal{C}} \newcommand{\Dd}{\mathcal{D}} \newcommand{\Ee}{\mathcal{E}} \newcommand{\Ff}{\mathcal{F}} \newcommand{\Gg}{\mathcal{G}} \newcommand{\Hh}{\mathcal{H}} \newcommand{\Ii}{\mathcal{I}} \newcommand{\Jj}{\mathcal{J}} \newcommand{\Kk}{\mathcal{K}} \newcommand{\Ll}{\mathcal{L}} \newcommand{\Mm}{\mathcal{M}} \newcommand{\Nn}{\mathcal{N}} \newcommand{\Oo}{\mathcal{O}} \newcommand{\Pp}{\mathcal{P}} \newcommand{\Qq}{\mathcal{Q}} \newcommand{\Rr}{\mathcal{R}} \newcommand{\Ss}{\mathcal{S}} \newcommand{\Tt}{\mathcal{T}} \newcommand{\Uu}{\mathcal{U}} \newcommand{\Vv}{\mathcal{V}} \newcommand{\Ww}{\mathcal{W}} \newcommand{\Xx}{\mathcal{X}} \newcommand{\Yy}{\mathcal{Y}} \newcommand{\Zz}{\mathcal{Z}} \newcommand{\al}{\alpha} \newcommand{\la}{\lambda} \newcommand{\ga}{\gamma} \newcommand{\Ga}{\Gamma} \newcommand{\La}{\Lambda} \newcommand{\Si}{\Sigma} \newcommand{\si}{\sigma} \newcommand{\be}{\beta} \newcommand{\de}{\delta} \newcommand{\De}{\Delta} \renewcommand{\phi}{\varphi} \renewcommand{\th}{\theta} \newcommand{\om}{\omega} \newcommand{\Om}{\Omega} \renewcommand{\epsilon}{\varepsilon} \newcommand{\Calpha}{\mathrm{C}^\al} \newcommand{\Cbeta}{\mathrm{C}^\be} \newcommand{\Cal}{\text{C}^\al} \newcommand{\Cdeux}{\text{C}^{2}} \newcommand{\Cun}{\text{C}^{1}} \newcommand{\Calt}[1]{\text{C}^{#1}} \newcommand{\lun}{\ell^1} \newcommand{\ldeux}{\ell^2} \newcommand{\linf}{\ell^\infty} \newcommand{\ldeuxj}{{\ldeux_j}} \newcommand{\Lun}{\text{\upshape L}^1} \newcommand{\Ldeux}{\text{\upshape L}^2} \newcommand{\Lp}{\text{\upshape L}^p} \newcommand{\Lq}{\text{\upshape L}^q} \newcommand{\Linf}{\text{\upshape L}^\infty} \newcommand{\lzero}{\ell^0} \newcommand{\lp}{\ell^p} \renewcommand{\d}{\ins{d}} \newcommand{\Grad}{\text{Grad}} \newcommand{\grad}{\text{grad}} \renewcommand{\div}{\text{div}} \newcommand{\diag}{\text{diag}} \newcommand{\pd}[2]{ \frac{ \partial #1}{\partial #2} } \newcommand{\pdd}[2]{ \frac{ \partial^2 #1}{\partial #2^2} } \newcommand{\dotp}[2]{\langle #1,\,#2\rangle} \newcommand{\norm}[1]{|\!| #1 |\!|} \newcommand{\normi}[1]{\norm{#1}_{\infty}} \newcommand{\normu}[1]{\norm{#1}_{1}} \newcommand{\normz}[1]{\norm{#1}_{0}} \newcommand{\abs}[1]{\vert #1 \vert} \newcommand{\argmin}{\text{argmin}} \newcommand{\argmax}{\text{argmax}} \newcommand{\uargmin}[1]{\underset{#1}{\argmin}\;} \newcommand{\uargmax}[1]{\underset{#1}{\argmax}\;} \newcommand{\umin}[1]{\underset{#1}{\min}\;} \newcommand{\umax}[1]{\underset{#1}{\max}\;} \newcommand{\pa}[1]{\left( #1 \right)} \newcommand{\choice}[1]{ \left\{ \begin{array}{l} #1 \end{array} \right. } \newcommand{\enscond}[2]{ \left\{ #1 \;:\; #2 \right\} } \newcommand{\qandq}{ \quad \text{and} \quad } \newcommand{\qqandqq}{ \qquad \text{and} \qquad } \newcommand{\qifq}{ \quad \text{if} \quad } \newcommand{\qqifqq}{ \qquad \text{if} \qquad } \newcommand{\qwhereq}{ \quad \text{where} \quad } \newcommand{\qqwhereqq}{ \qquad \text{where} \qquad } \newcommand{\qwithq}{ \quad \text{with} \quad } \newcommand{\qqwithqq}{ \qquad \text{with} \qquad } \newcommand{\qforq}{ \quad \text{for} \quad } \newcommand{\qqforqq}{ \qquad \text{for} \qquad } \newcommand{\qqsinceqq}{ \qquad \text{since} \qquad } \newcommand{\qsinceq}{ \quad \text{since} \quad } \newcommand{\qarrq}{\quad\Longrightarrow\quad} \newcommand{\qqarrqq}{\quad\Longrightarrow\quad} \newcommand{\qiffq}{\quad\Longleftrightarrow\quad} \newcommand{\qqiffqq}{\qquad\Longleftrightarrow\qquad} \newcommand{\qsubjq}{ \quad \text{subject to} \quad } \newcommand{\qqsubjqq}{ \qquad \text{subject to} \qquad } \]

Geodesic Mesh Processing

Geodesic Mesh Processing

This tour explores geodesic computations on 3D meshes.

Contents

Installing toolboxes and setting up the path.

You need to download the following files: signal toolbox, general toolbox, graph toolbox and wavelet_meshes toolbox.

You need to unzip these toolboxes in your working directory, so that you have toolbox_signal, toolbox_general, toolbox_graph and toolbox_wavelet_meshes in your directory.

For Scilab user: you must replace the Matlab comment '%' by its Scilab counterpart '//'.

Recommandation: You should create a text file named for instance numericaltour.sce (in Scilab) or numericaltour.m (in Matlab) to write all the Scilab/Matlab command you want to execute. Then, simply run exec('numericaltour.sce'); (in Scilab) or numericaltour; (in Matlab) to run the commands.

Execute this line only if you are using Matlab.

getd = @(p)path(p,path); % scilab users must *not* execute this

Then you can add the toolboxes to the path.

getd('toolbox_signal/');
getd('toolbox_general/');
getd('toolbox_graph/');
getd('toolbox_wavelet_meshes/');

Distance Computation on 3D Meshes

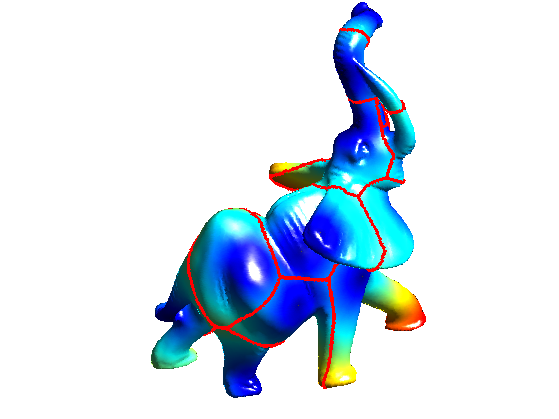
Using the fast marching on a triangulated surface, one can compute the distance from a set of input points. This function also returns the segmentation of the surface into geodesic Voronoi cells.

Load a 3D mesh.

name = 'elephant-50kv';
[vertex,faces] = read_mesh(name);
nvert = size(vertex,2);

Starting points for the distance computation.

nstart = 15;
pstarts = floor(rand(nstart,1)*nvert)+1;
options.start_points = pstarts;

No end point for the propagation.

clear options;
options.end_points = [];

Use a uniform, constant, metric for the propagation.

options.W = ones(nvert,1);

Compute the distance using Fast Marching.

options.nb_iter_max = Inf;
[D,S,Q] = perform_fast_marching_mesh(vertex, faces, pstarts, options);

Display the distance on the 3D mesh.

clf;
plot_fast_marching_mesh(vertex,faces, D, [], options);

Extract precisely the voronoi regions, and display it.

[Qexact,DQ, voronoi_edges] = compute_voronoi_mesh(vertex, faces, pstarts, options);
options.voronoi_edges = voronoi_edges;
plot_fast_marching_mesh(vertex,faces, D, [], options);

Exercice 1: (check the solution) Using options.nb_iter_max, display the progression of the propagation. 

exo1;

Geodesic Path Extraction

Geodesic path are extracted using gradient descent of the distance map.

Select random endding points, from which the geodesic curves start.

nend = 40;
pend = floor(rand(nend,1)*nvert)+1;

Compute the vertices 1-ring.

vring = compute_vertex_ring(faces);

Exercice 2: (check the solution) For each point pend(k), compute a discrete geodesic path path such that path(1)=pend(k) and D(path(i+1))<D(path(i)) with [path(i), path(i+1)] being an edge of the mesh. This means that path(i+1) is an element of vring{path(i)}. Display the paths on the mesh. 

exo2;

In order to extract a smooth path, one needs to use a gradient descent.

options.method = 'continuous';
paths = compute_geodesic_mesh(D, vertex, faces, pend, options);

Display the smooth paths.

plot_fast_marching_mesh(vertex,faces, Q, paths, options);

Curvature-based Speed Functions

In order to extract salient features of a surface, one can define a speed function that depends on some curvature measure of the surface.

Load a mesh with sharp features.

clear options;
name = 'fandisk';
[vertex,faces] = read_mesh(name);
options.name = name;
nvert = size(vertex,2);

Display it.

clf;
plot_mesh(vertex,faces, options);

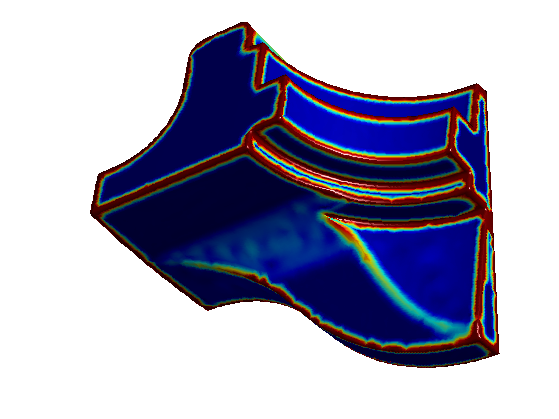
Compute the curvature.

options.verb = 0;
[Umin,Umax,Cmin,Cmax] = compute_curvature(vertex,faces,options);

Compute some absolute measure of curvature.

C = abs(Cmin)+abs(Cmax);
C = min(C,.1);

Display the curvature on the surface

options.face_vertex_color = rescale(C);
clf;
plot_mesh(vertex,faces,options);
colormap jet(256);

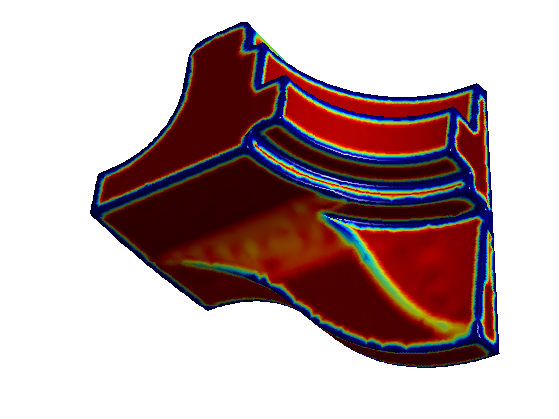
Compute a metric that depends on the curvature. Should be small in area that the geodesic should follow.

epsilon = .5;
W = rescale(-min(C,0.1), .1,1);

Display the metric on the surface

options.face_vertex_color = rescale(W);
clf;
plot_mesh(vertex,faces,options);
colormap jet(256);

Starting points.

pstarts = [2564; 16103; 15840];
options.start_points = pstarts;

Compute the distance using Fast Marching.

options.W = W;
options.nb_iter_max = Inf;
[D,S,Q] = perform_fast_marching_mesh(vertex, faces, pstarts, options);

Display the distance on the 3D mesh.

options.colorfx = 'equalize';
clf;
plot_fast_marching_mesh(vertex,faces, D, [], options);

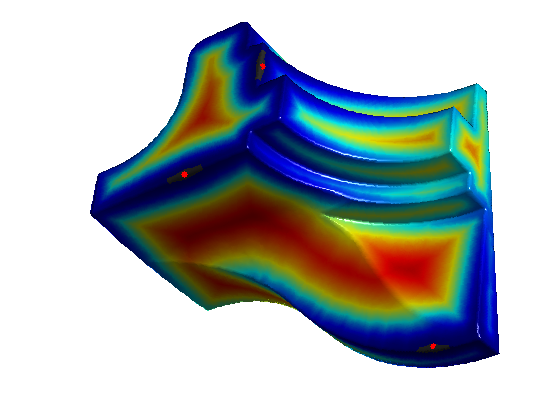
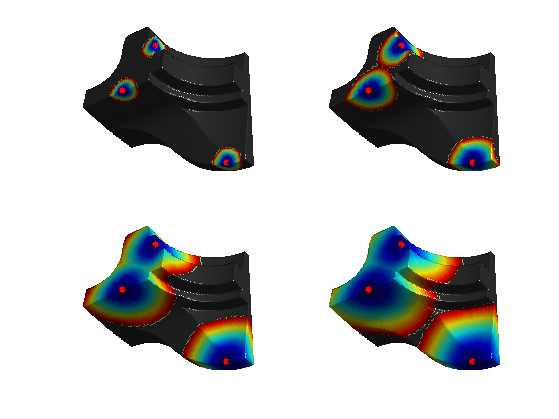
Exercice 3: (check the solution) Using options.nb_iter_max, display the progression of the propagation for constant W. 

exo3;

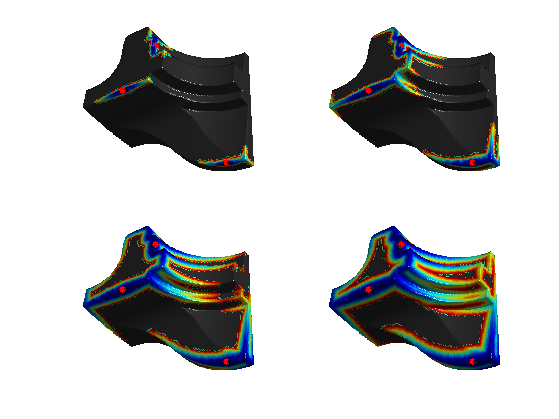
Exercice 4: (check the solution) Using options.nb_iter_max, display the progression of the propagation for a curvature based W. 

exo4;

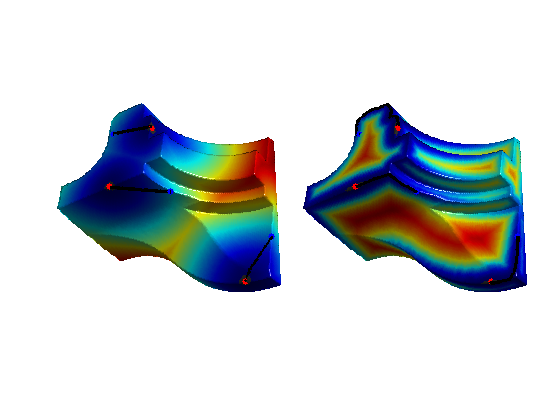
Exercice 5: (check the solution) Extract geodesics. 

exo5;

Texture-based Speed Functions

One can take into account a texture to design the speed function.

clear options;
options.base_mesh = 'ico';
options.relaxation = 1;
options.keep_subdivision = 0;
[vertex,faces] = compute_semiregular_sphere(7,options);
nvert = size(vertex,2);

Load a function on the mesh.

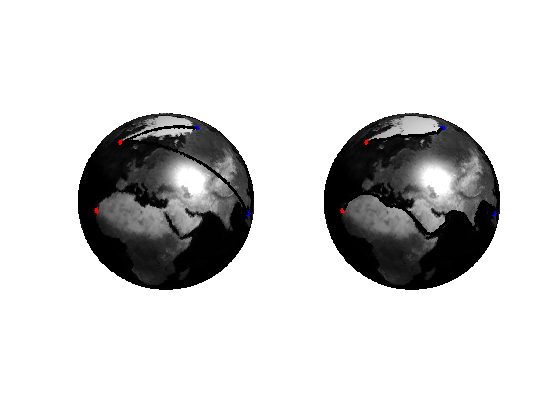
name = 'earth';
f = load_spherical_function(name, vertex, options);
options.name = name;

Starting points.

pstarts = [2844; 5777];
options.start_points = pstarts;

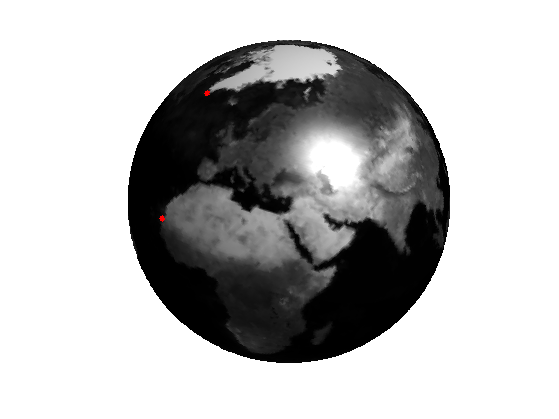
Display the function.

clf;
plot_fast_marching_mesh(vertex,faces, f, [], options);
colormap gray(256);

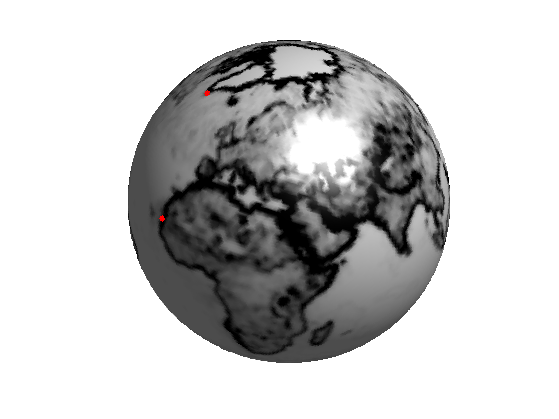
Load and display the gradient magnitude of the function.

g = load_spherical_function('earth-grad', vertex, options);

Display it.

clf;
plot_fast_marching_mesh(vertex,faces, g, [], options);
colormap gray(256);

Design a metric.

W = rescale(-min(g,10),0.01,1);

Display it.

clf;
plot_fast_marching_mesh(vertex,faces, W, [], options);
colormap gray(256);

Exercice 6: (check the solution) Using options.nb_iter_max, display the progression of the propagation for a curvature based W. 

exo6;

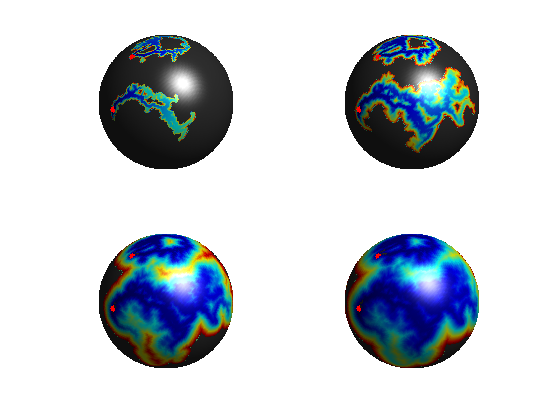
Exercice 7: (check the solution) Extract geodesics. 

exo7;


Copyright (c) 2010 Gabriel Peyre