\[ \newcommand{\NN}{\mathbb{N}} \newcommand{\CC}{\mathbb{C}} \newcommand{\GG}{\mathbb{G}} \newcommand{\LL}{\mathbb{L}} \newcommand{\PP}{\mathbb{P}} \newcommand{\QQ}{\mathbb{Q}} \newcommand{\RR}{\mathbb{R}} \newcommand{\VV}{\mathbb{V}} \newcommand{\ZZ}{\mathbb{Z}} \newcommand{\FF}{\mathbb{F}} \newcommand{\KK}{\mathbb{K}} \newcommand{\UU}{\mathbb{U}} \newcommand{\EE}{\mathbb{E}} \newcommand{\Aa}{\mathcal{A}} \newcommand{\Bb}{\mathcal{B}} \newcommand{\Cc}{\mathcal{C}} \newcommand{\Dd}{\mathcal{D}} \newcommand{\Ee}{\mathcal{E}} \newcommand{\Ff}{\mathcal{F}} \newcommand{\Gg}{\mathcal{G}} \newcommand{\Hh}{\mathcal{H}} \newcommand{\Ii}{\mathcal{I}} \newcommand{\Jj}{\mathcal{J}} \newcommand{\Kk}{\mathcal{K}} \newcommand{\Ll}{\mathcal{L}} \newcommand{\Mm}{\mathcal{M}} \newcommand{\Nn}{\mathcal{N}} \newcommand{\Oo}{\mathcal{O}} \newcommand{\Pp}{\mathcal{P}} \newcommand{\Qq}{\mathcal{Q}} \newcommand{\Rr}{\mathcal{R}} \newcommand{\Ss}{\mathcal{S}} \newcommand{\Tt}{\mathcal{T}} \newcommand{\Uu}{\mathcal{U}} \newcommand{\Vv}{\mathcal{V}} \newcommand{\Ww}{\mathcal{W}} \newcommand{\Xx}{\mathcal{X}} \newcommand{\Yy}{\mathcal{Y}} \newcommand{\Zz}{\mathcal{Z}} \newcommand{\al}{\alpha} \newcommand{\la}{\lambda} \newcommand{\ga}{\gamma} \newcommand{\Ga}{\Gamma} \newcommand{\La}{\Lambda} \newcommand{\Si}{\Sigma} \newcommand{\si}{\sigma} \newcommand{\be}{\beta} \newcommand{\de}{\delta} \newcommand{\De}{\Delta} \renewcommand{\phi}{\varphi} \renewcommand{\th}{\theta} \newcommand{\om}{\omega} \newcommand{\Om}{\Omega} \renewcommand{\epsilon}{\varepsilon} \newcommand{\Calpha}{\mathrm{C}^\al} \newcommand{\Cbeta}{\mathrm{C}^\be} \newcommand{\Cal}{\text{C}^\al} \newcommand{\Cdeux}{\text{C}^{2}} \newcommand{\Cun}{\text{C}^{1}} \newcommand{\Calt}[1]{\text{C}^{#1}} \newcommand{\lun}{\ell^1} \newcommand{\ldeux}{\ell^2} \newcommand{\linf}{\ell^\infty} \newcommand{\ldeuxj}{{\ldeux_j}} \newcommand{\Lun}{\text{\upshape L}^1} \newcommand{\Ldeux}{\text{\upshape L}^2} \newcommand{\Lp}{\text{\upshape L}^p} \newcommand{\Lq}{\text{\upshape L}^q} \newcommand{\Linf}{\text{\upshape L}^\infty} \newcommand{\lzero}{\ell^0} \newcommand{\lp}{\ell^p} \renewcommand{\d}{\ins{d}} \newcommand{\Grad}{\text{Grad}} \newcommand{\grad}{\text{grad}} \renewcommand{\div}{\text{div}} \newcommand{\diag}{\text{diag}} \newcommand{\pd}[2]{ \frac{ \partial #1}{\partial #2} } \newcommand{\pdd}[2]{ \frac{ \partial^2 #1}{\partial #2^2} } \newcommand{\dotp}[2]{\langle #1,\,#2\rangle} \newcommand{\norm}[1]{|\!| #1 |\!|} \newcommand{\normi}[1]{\norm{#1}_{\infty}} \newcommand{\normu}[1]{\norm{#1}_{1}} \newcommand{\normz}[1]{\norm{#1}_{0}} \newcommand{\abs}[1]{\vert #1 \vert} \newcommand{\argmin}{\text{argmin}} \newcommand{\argmax}{\text{argmax}} \newcommand{\uargmin}[1]{\underset{#1}{\argmin}\;} \newcommand{\uargmax}[1]{\underset{#1}{\argmax}\;} \newcommand{\umin}[1]{\underset{#1}{\min}\;} \newcommand{\umax}[1]{\underset{#1}{\max}\;} \newcommand{\pa}[1]{\left( #1 \right)} \newcommand{\choice}[1]{ \left\{ \begin{array}{l} #1 \end{array} \right. } \newcommand{\enscond}[2]{ \left\{ #1 \;:\; #2 \right\} } \newcommand{\qandq}{ \quad \text{and} \quad } \newcommand{\qqandqq}{ \qquad \text{and} \qquad } \newcommand{\qifq}{ \quad \text{if} \quad } \newcommand{\qqifqq}{ \qquad \text{if} \qquad } \newcommand{\qwhereq}{ \quad \text{where} \quad } \newcommand{\qqwhereqq}{ \qquad \text{where} \qquad } \newcommand{\qwithq}{ \quad \text{with} \quad } \newcommand{\qqwithqq}{ \qquad \text{with} \qquad } \newcommand{\qforq}{ \quad \text{for} \quad } \newcommand{\qqforqq}{ \qquad \text{for} \qquad } \newcommand{\qqsinceqq}{ \qquad \text{since} \qquad } \newcommand{\qsinceq}{ \quad \text{since} \quad } \newcommand{\qarrq}{\quad\Longrightarrow\quad} \newcommand{\qqarrqq}{\quad\Longrightarrow\quad} \newcommand{\qiffq}{\quad\Longleftrightarrow\quad} \newcommand{\qqiffqq}{\qquad\Longleftrightarrow\qquad} \newcommand{\qsubjq}{ \quad \text{subject to} \quad } \newcommand{\qqsubjqq}{ \qquad \text{subject to} \qquad } \]

1-D Haar Wavelets

1-D Haar Wavelets

This numerical tour explores 1-D multiresolution analysis with Haar transform. It was introduced in 1910 by Haar [Haar1910] and is arguably the first example of wavelet basis.

Contents

Installing toolboxes and setting up the path.

You need to download the following files: signal toolbox and general toolbox.

You need to unzip these toolboxes in your working directory, so that you have toolbox_signal and toolbox_general in your directory.

For Scilab user: you must replace the Matlab comment '%' by its Scilab counterpart '//'.

Recommandation: You should create a text file named for instance numericaltour.sce (in Scilab) or numericaltour.m (in Matlab) to write all the Scilab/Matlab command you want to execute. Then, simply run exec('numericaltour.sce'); (in Scilab) or numericaltour; (in Matlab) to run the commands.

Execute this line only if you are using Matlab.

getd = @(p)path(p,path); % scilab users must *not* execute this

Then you can add the toolboxes to the path.

getd('toolbox_signal/');
getd('toolbox_general/');

Forward Haar Transform

The Haar transform is the simplest orthogonal wavelet transform. It is computed by iterating difference and averaging between odd and even samples of the signal.

Size \(N\) of the signal.

N = 512;

First we load a 1-D signal \(f \in \RR^N\).

name = 'piece-regular';
f = rescale( load_signal(name, N) );

The Haar transform operates over \(J = \log_2(N)-1\) scales. It computes a series of coarse scale and fine scale coefficients \(a_j, d_j \in \RR^{N_j}\) where \(N_j=2^j\). 

J = log2(N)-1;

The forward Haar transform computed \( \Hh(f) = (d_j)_{j=0}^J \cup \{a_0\} \). Note that the set of coarse scale coefficients \((a_j)_{j>0}\) are not stored.

This transform is orthogonal, meaning \( \Hh \circ \Hh^* = \text{Id} \), and that there is the following conservation of energy \[ \sum_i \abs{f_i}^2 = \norm{f}^2 = \norm{\Hh f}^2 = \sum_j \norm{d_j}^2 + \abs{a_0}^2. \]

One initilizes the algorithm with \(a_{J+1}=f\). The set of coefficients \(d_{j},a_j\) are computed from \(a_{j+1}\) as \[ \forall k=0,\ldots,2^j-1, \quad a_j[k] = \frac{a_{j+1}[2k] + a_{j+1}[2k+1]}{\sqrt{2}} \qandq d_j[k] = \frac{a_{j+1}[2k] - a_{j+1}[2k+1]}{\sqrt{2}}. \]

Shortcut to compute \(a_j, d_j\) from \(a_{j+1}\).

haar = @(a)[   a(1:2:length(a)) + a(2:2:length(a));
                    a(1:2:length(a)) - a(2:2:length(a)) ]/sqrt(2);

Display the result of the one step of the transform.

clf;
subplot(2,1,1);
plot(f); axis('tight'); title('Signal');
subplot(2,1,2);
plot(haar(f)); axis('tight'); title('Transformed');

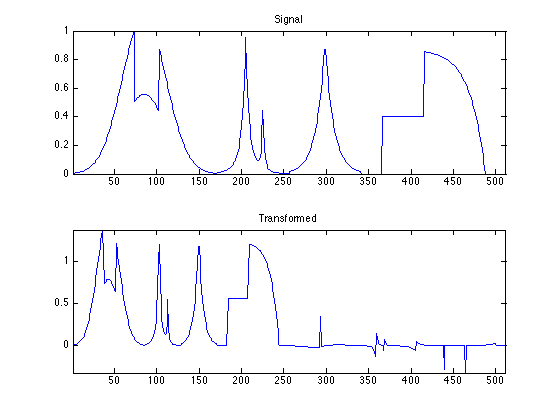
The output of the forward transform is stored in the variable fw. At a given iteration indexed by a scale j, it will store in fw(1:2^(j+1)) the variable \(a_{j+1}\), and in the remaining entries the variable \(d_{j+1},d_{j+2},\ldots,d_J\).

Initializes the algorithm at scale \(j=J\).

j = J;

Initialize fw to the full signal. 

fw = f;

At iteration indexed by \(j\), select the sub-part of the signal containing \(a_{j+1}\), and apply it the Haar operator.

fw(1:2^(j+1)) = haar(fw(1:2^(j+1)));

Display the signal and its coarse coefficients.

s = 400; t = 40;
clf;
subplot(2,1,1);
plot(f,'.-'); axis([s-t s+t 0 1]); title('Signal (zoom)');
subplot(2,1,2);
plot(fw(1:2^j),'.-'); axis([(s-t)/2 (s+t)/2 min(fw(1:2^j)) max(fw(1:2^j))]); title('Averages (zoom)');

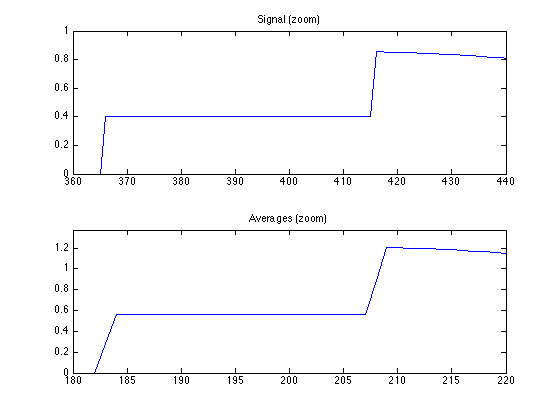
Exercice 1: (check the solution) Implement a full wavelet Haar transform that extract iteratively wavelet coefficients, by repeating these steps. Take care of choosing the correct number of steps. 

exo1;

Check that the transform is orthogonal, which means that the energy of the coefficient is the same as the energy of the signal.

fprintf('Should be 0: %.3f.\n', (norm(f)-norm(fw))/norm(f));

Should be 0: 0.000.

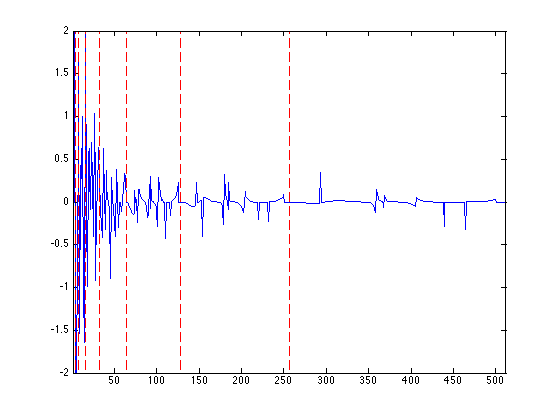
We display the whole set of coefficients fw, with red vertical separator between the scales. Can you recognize where are the low frequencies and the high frequencies? 

clf;
plot_wavelet(fw);
axis([1 N -2 2]);

Backward Haar Transform

The backward transform computes a signal \(f_1 = \Hh^*(h)\) from a set of coefficients \( h = (d_j)_{j=0}^J \cup \{a_0\} \)

If \(h = \Hh(f)\) are the coefficients of a signal \(f\), one recovers \( f_1 = f \).

The inverse transform starts from \(j=0\), and computes \(a_{j+1}\) from the knowledge of \(a_j,d_j\) as \[ \forall k = 0,\ldots,2^j-1, \quad a_{j+1}[2k] = \frac{ a_j[k] + d_j[k] }{\sqrt{2}} a_{j+1}[2k+1] = \frac{ a_j[k] - d_j[k] }{\sqrt{2}} \]

One step of inverse transform

ihaar = @(a,d)assign( zeros(2*length(a),1), ...
        [1:2:2*length(a), 2:2:2*length(a)], [a+d; a-d]/sqrt(2) );

Initialize the signal to recover \(f_1\) as the transformed coefficient, and select the smallest possible scale \(j=0\).

f1 = fw;
j = 0;

Apply one step of inverse transform.

f1(1:2^(j+1)) = ihaar(f1(1:2^j), f1(2^j+1:2^(j+1)));

Exercice 2: (check the solution) Write the inverse wavelet transform that computes f1 from the coefficients fw. 

exo2;

Check that we have correctly recovered the signal.

fprintf('Should be 0: %.3f.\n', (norm(f-f1))/norm(f));

Should be 0: 0.000.

Haar Linear Approximation

Linear approximation is obtained by setting to zeros the Haar coefficient coefficients above a certain scale \(j\).

Cut-off scale.

j = J-1;

Set to zero fine scale coefficients.

fw1 = fw; fw1(2^j+1:end) = 0;

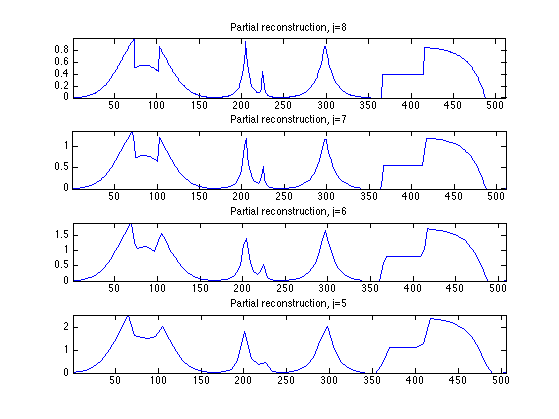
Computing the signal \(f_1\) corresponding to these coefficients fw1 computes the orthogonal projection on the space of signal that are constant on disjoint intervals of length \(N/2^j\).

Exercice 3: (check the solution) Display the reconstructed signal obtained from fw1, for a decreasing cut-off scale \(j\). 

exo3;

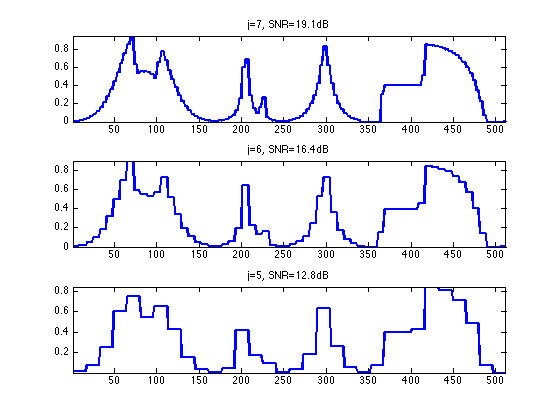
Haar Non-linear Approximation

Non-linear approximation is obtained by thresholding low amplitude wavelet coefficients. It is defined as \[ f_T = \Hh^* \circ S_T \circ \Hh(f) \] where \(S_T\) is the hard tresholding operator \[ S_T(x)_i = \choice{ x_i \qifq \abs{x_i}>T, \\ 0 \quad \text{otherwise}. }. \] 

S = @(x,T) x .* (abs(x)>T);

Set the threshold value.

T = .5;

Threshold the coefficients.

fwT = S(fw,T);

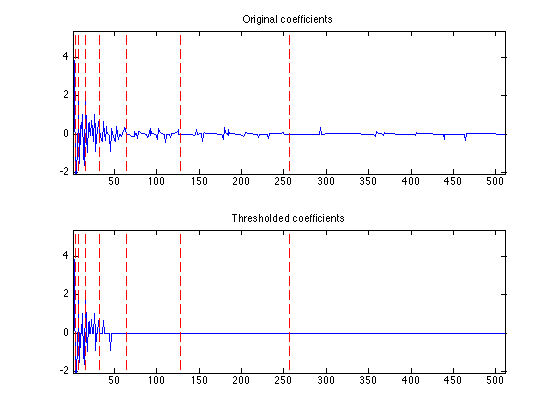
Display the coefficients before and after thresholding.

clf;
subplot(2,1,1);
plot_wavelet(fw); axis('tight'); title('Original coefficients');
subplot(2,1,2);
plot_wavelet(fwT); axis('tight'); title('Thresholded coefficients');

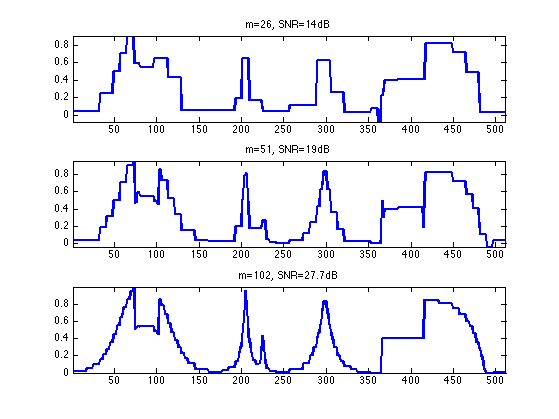
Exercice 4: (check the solution) Find the threshold \(T\) so that the number of remaining coefficients in fwT is a fixed number \(m\). Use this threshold to compute fwT and then display the corresponding approximation \(f_1\) of \(f\). Try for an increasing number \(m\) of coeffiients. 

exo4;

The Shape of a Wavelet

A wavelet coefficient corresponds to an inner product of \(f\) with a wavelet Haar atom \(\psi_{j,k}\) \[ d_j[k] = \dotp{f}{\psi_{j,k}} \]

The wavelet \(\psi_{j,k}\) can be computed by applying the inverse wavelet transform to fw where fw[m]=1 and fw[s]=0 for \(s \neq m\) where \(m = 2^j+k\).

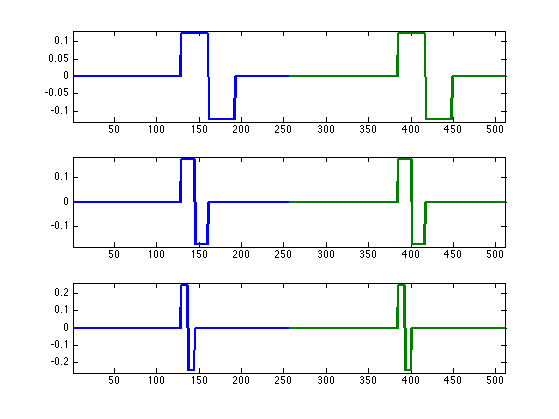
Exercice 5: (check the solution) Compute wavelets at several positions and scales. 

exo5;

Bibliography


Copyright (c) 2010 Gabriel Peyre