\[ \newcommand{\NN}{\mathbb{N}} \newcommand{\CC}{\mathbb{C}} \newcommand{\GG}{\mathbb{G}} \newcommand{\LL}{\mathbb{L}} \newcommand{\PP}{\mathbb{P}} \newcommand{\QQ}{\mathbb{Q}} \newcommand{\RR}{\mathbb{R}} \newcommand{\VV}{\mathbb{V}} \newcommand{\ZZ}{\mathbb{Z}} \newcommand{\FF}{\mathbb{F}} \newcommand{\KK}{\mathbb{K}} \newcommand{\UU}{\mathbb{U}} \newcommand{\EE}{\mathbb{E}} \newcommand{\Aa}{\mathcal{A}} \newcommand{\Bb}{\mathcal{B}} \newcommand{\Cc}{\mathcal{C}} \newcommand{\Dd}{\mathcal{D}} \newcommand{\Ee}{\mathcal{E}} \newcommand{\Ff}{\mathcal{F}} \newcommand{\Gg}{\mathcal{G}} \newcommand{\Hh}{\mathcal{H}} \newcommand{\Ii}{\mathcal{I}} \newcommand{\Jj}{\mathcal{J}} \newcommand{\Kk}{\mathcal{K}} \newcommand{\Ll}{\mathcal{L}} \newcommand{\Mm}{\mathcal{M}} \newcommand{\Nn}{\mathcal{N}} \newcommand{\Oo}{\mathcal{O}} \newcommand{\Pp}{\mathcal{P}} \newcommand{\Qq}{\mathcal{Q}} \newcommand{\Rr}{\mathcal{R}} \newcommand{\Ss}{\mathcal{S}} \newcommand{\Tt}{\mathcal{T}} \newcommand{\Uu}{\mathcal{U}} \newcommand{\Vv}{\mathcal{V}} \newcommand{\Ww}{\mathcal{W}} \newcommand{\Xx}{\mathcal{X}} \newcommand{\Yy}{\mathcal{Y}} \newcommand{\Zz}{\mathcal{Z}} \newcommand{\al}{\alpha} \newcommand{\la}{\lambda} \newcommand{\ga}{\gamma} \newcommand{\Ga}{\Gamma} \newcommand{\La}{\Lambda} \newcommand{\Si}{\Sigma} \newcommand{\si}{\sigma} \newcommand{\be}{\beta} \newcommand{\de}{\delta} \newcommand{\De}{\Delta} \renewcommand{\phi}{\varphi} \renewcommand{\th}{\theta} \newcommand{\om}{\omega} \newcommand{\Om}{\Omega} \renewcommand{\epsilon}{\varepsilon} \newcommand{\Calpha}{\mathrm{C}^\al} \newcommand{\Cbeta}{\mathrm{C}^\be} \newcommand{\Cal}{\text{C}^\al} \newcommand{\Cdeux}{\text{C}^{2}} \newcommand{\Cun}{\text{C}^{1}} \newcommand{\Calt}[1]{\text{C}^{#1}} \newcommand{\lun}{\ell^1} \newcommand{\ldeux}{\ell^2} \newcommand{\linf}{\ell^\infty} \newcommand{\ldeuxj}{{\ldeux_j}} \newcommand{\Lun}{\text{\upshape L}^1} \newcommand{\Ldeux}{\text{\upshape L}^2} \newcommand{\Lp}{\text{\upshape L}^p} \newcommand{\Lq}{\text{\upshape L}^q} \newcommand{\Linf}{\text{\upshape L}^\infty} \newcommand{\lzero}{\ell^0} \newcommand{\lp}{\ell^p} \renewcommand{\d}{\ins{d}} \newcommand{\Grad}{\text{Grad}} \newcommand{\grad}{\text{grad}} \renewcommand{\div}{\text{div}} \newcommand{\diag}{\text{diag}} \newcommand{\pd}[2]{ \frac{ \partial #1}{\partial #2} } \newcommand{\pdd}[2]{ \frac{ \partial^2 #1}{\partial #2^2} } \newcommand{\dotp}[2]{\langle #1,\,#2\rangle} \newcommand{\norm}[1]{|\!| #1 |\!|} \newcommand{\normi}[1]{\norm{#1}_{\infty}} \newcommand{\normu}[1]{\norm{#1}_{1}} \newcommand{\normz}[1]{\norm{#1}_{0}} \newcommand{\abs}[1]{\vert #1 \vert} \newcommand{\argmin}{\text{argmin}} \newcommand{\argmax}{\text{argmax}} \newcommand{\uargmin}[1]{\underset{#1}{\argmin}\;} \newcommand{\uargmax}[1]{\underset{#1}{\argmax}\;} \newcommand{\umin}[1]{\underset{#1}{\min}\;} \newcommand{\umax}[1]{\underset{#1}{\max}\;} \newcommand{\pa}[1]{\left( #1 \right)} \newcommand{\choice}[1]{ \left\{ \begin{array}{l} #1 \end{array} \right. } \newcommand{\enscond}[2]{ \left\{ #1 \;:\; #2 \right\} } \newcommand{\qandq}{ \quad \text{and} \quad } \newcommand{\qqandqq}{ \qquad \text{and} \qquad } \newcommand{\qifq}{ \quad \text{if} \quad } \newcommand{\qqifqq}{ \qquad \text{if} \qquad } \newcommand{\qwhereq}{ \quad \text{where} \quad } \newcommand{\qqwhereqq}{ \qquad \text{where} \qquad } \newcommand{\qwithq}{ \quad \text{with} \quad } \newcommand{\qqwithqq}{ \qquad \text{with} \qquad } \newcommand{\qforq}{ \quad \text{for} \quad } \newcommand{\qqforqq}{ \qquad \text{for} \qquad } \newcommand{\qqsinceqq}{ \qquad \text{since} \qquad } \newcommand{\qsinceq}{ \quad \text{since} \quad } \newcommand{\qarrq}{\quad\Longrightarrow\quad} \newcommand{\qqarrqq}{\quad\Longrightarrow\quad} \newcommand{\qiffq}{\quad\Longleftrightarrow\quad} \newcommand{\qqiffqq}{\qquad\Longleftrightarrow\qquad} \newcommand{\qsubjq}{ \quad \text{subject to} \quad } \newcommand{\qqsubjqq}{ \qquad \text{subject to} \qquad } \newcommand{\eqdef}{\equiv} \]

Neural Networks

Neural Networks

This tour details fully connected multi-layers neural netorks.

Contents

We recommend that after doing this Numerical Tours, you apply it to your own data, for instance using a dataset from LibSVM.

Disclaimer: these machine learning tours are intended to be overly-simplistic implementations and applications of baseline machine learning methods. For more advanced uses and implementations, we recommend to use a state-of-the-art library, the most well known being Scikit-Learn

Installing toolboxes and setting up the path.

You need to download the following files: general toolbox.

You need to unzip these toolboxes in your working directory, so that you have toolbox_general in your directory.

For Scilab user: you must replace the Matlab comment '%' by its Scilab counterpart '//'.

Recommandation: You should create a text file named for instance numericaltour.sce (in Scilab) or numericaltour.m (in Matlab) to write all the Scilab/Matlab command you want to execute. Then, simply run exec('numericaltour.sce'); (in Scilab) or numericaltour; (in Matlab) to run the commands.

Execute this line only if you are using Matlab.

getd = @(p)path(p,path); % scilab users must *not* execute this

Then you can add the toolboxes to the path.

getd('toolbox_general/');

Some useful helpers.

dotp = @(x,y)sum(x(:).*y(:));
max2 = @(S)repmat(max(S,[],2), [1 size(S,2)]);
SM = @(S)exp(S) ./ repmat( sum(exp(S),2), [1 size(S,2)]);
SM = @(S)SM(S-max2(S));

Dataset Generation

Build a synthetic data set for classification

Generate Data

n0 = 100; % number of points per class
p = 2;   % dimensionality
k = 3;   % number of classes
n = n0*k; % Total number of points
x = zeros(p,n);
y = zeros(1,n);
for j=1:k
    I = n0*(j-1)+1:n0*j;
    r = linspace(0.0,1,n0); % radius
    t = linspace(j*4,(j+1)*4,n0) + randn(1,n0)*0.2; % angle
    x(:,I) = [r.*sin(t); r.*cos(t)];
    y(1,I) = j;
end

Display.

col = {'r' 'g' 'b'};
clf;  hold on;
for j=1:k
    I = find(y==j);
    plot(x(1,I), x(2,I), '.', 'color', col{j}, 'MarkerSize', 20);
end
axis equal; axis off;

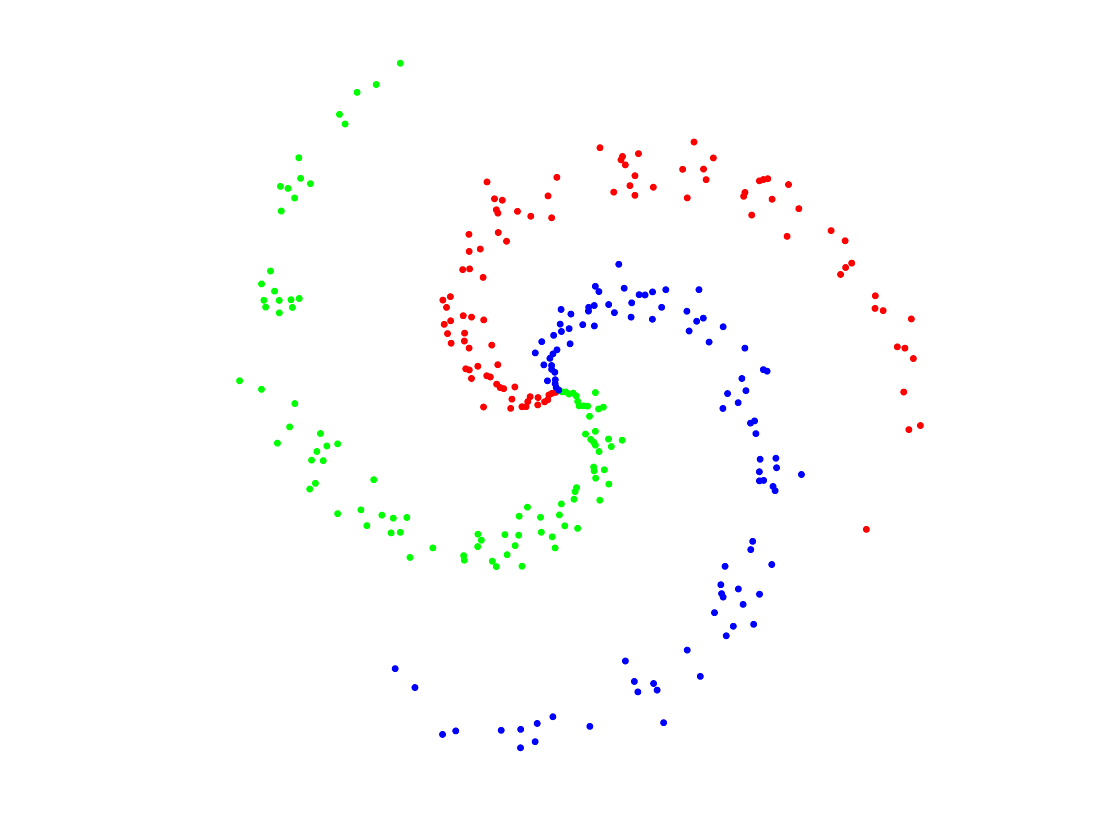
Class probability matrix.

Y = double( repmat((1:k)', [1,n]) == repmat(y, [k,1]) );

Building the Network

We setup the network. It is parameterized by the dimensions of the layers.

The network is composed of \(R\) layers, and operate by initialyzing \(x_0=x\) and then iterating \[ \forall r=0,\ldots,R, \quad x_{r+1} \eqdef \rho(A_r x_r + b_r). \] Here \(\rho : \RR \mapsto \RR\) is a non-linear activation function which operate coordinate by coordinate. The intermediate variables are \(x_r \in \RR^{d_r}\) with \((d_0,d_{L+1})=(p,k)\). The matrices have size \(A_r \in \RR^{d_{r+1} \times d_r}\) while the biases have size \(b_r \in \RR^{d_{r+1}}\).

The final value is obtained by comparing the predicted value \(x_{R+1}\) to the data \(y\) using some loss function \[ \ell \eqdef \Ll(x_{R+1},y). \]

Load the loss and its gradient. Here we use a multi-class logistic loss \[ \Ll(z,y) \eqdef \log \sum_{i=1}^k e^{z_i} - \dotp{z}{y}. \]

Note that in practice the computation is done in parallel over an array \(x\) of size \((p,n)\) of \(n\) points in \(\RR^p\), where the class probability to predict is an array \(y\) of size \(k,n\) where \(k\) is the number of classes. 

dotp = @(x,y)sum(x(:).*y(:));
max2 = @(S)repmat(max(S,[],2), [1 size(S,2)]);
% stabilized log-sum-exp
LSE = @(S)log( sum(exp(S), 2) );
LSE = @(S)LSE( S-max2(S) ) + max(S,[],2);
% stabilized soft-max
SM = @(S)exp(S) ./ repmat( sum(exp(S),2), [1 size(S,2)]);
SM = @(S)SM(S-max2(S));
% energy, y being a target probability distribution
loss.F = @(z,y)sum(LSE(z')) - dotp(z,y);
% gradient
loss.G = @(z,y)SM(z')' -  y;

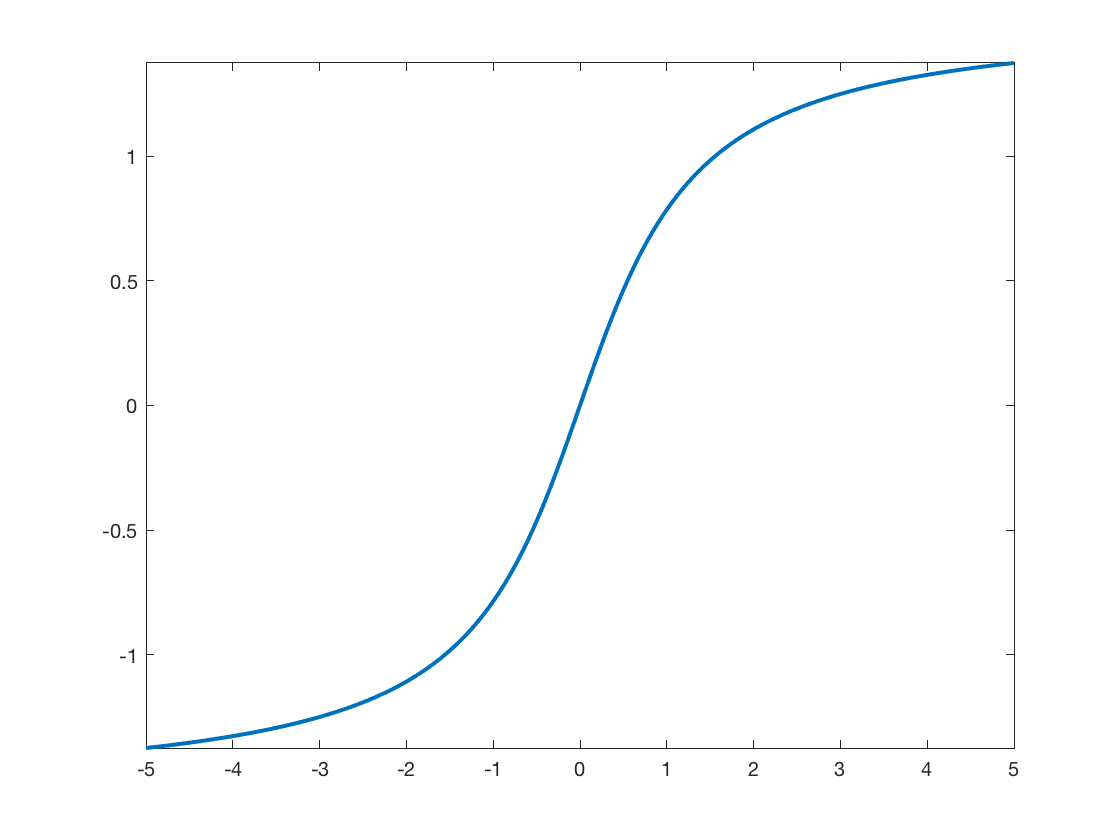
Load the activation function. Here we use an atan sigmoid function.

rho.F  = @(u)atan(u);
rho.G = @(u)1./(1+u.^2);

Display the activation.

t = linspace(-5,5,201);
clf;
plot(t, rho.F(t), 'LineWidth', 2);
axis tight;

Dimensions \(d_r\) of the layers.

D = [p 15 k]; % here a single hidden layer

Initialize the layers randomly.

R = length(D)-1;
A = {}; b = {};
for r=1:R
    A{r} = randn(D(r+1),D(r));
    b{r} = randn(D(r+1),1);
end

Evaluate the network. Bookkeep the intermediate results: this is crucial for the computation of the gradient.

X = {};
X{1} = x;
for r=1:R
    X{r+1} = rho.F( A{r}*X{r}+repmat(b{r},[1 n]) );
end
L = loss.F(X{R+1},Y);

Network Optimization

The network parameters are optimized by minimizing the non-convex empirical loss minimization through gradient descent.

Initialize the gradient as \[ \nabla_{x_{R+1}} \ell = \nabla \Ll(x_{R+1},y) \]

gx = loss.G(X{R+1},Y);

The successive gradient with respect to the intermediate variables \(x_r\) are solutions of a backward recursion, which corresponds to the celebrated backpropagation algorithm. \[ \forall r=R,\ldots,1, \quad \nabla_{x_{r}} \ell = A_r^\top M_r \] where we denoted \[ M_r \eqdef \rho'(A_r x_r + b_r ) \odot \nabla_{x_{r+1}} \ell, \] where \(\odot\) is entry-wise multiplications.

From these gradients with respect to the intermediate layers variables, the gradient with respect to the network paramters are retrieved as \[ \nabla_{A_r} \ell = M_r x_r^\top, \qandq \nabla_{b_r} \ell = M_r 1_n. \]

Perform the back-propagation.

gA = {}; gb = {};
for r=R:-1:1
    M = rho.G(A{r}*X{r}+repmat(b{r},[1 n])) .* gx;
    % nabla_X{r}
    gx = A{r}' * M;
    % nabla_A{r}
    gA{r} =  M * X{r}';
    % nabla_b{r}
    gb{r} =  sum(M,2);
end

Exercice 1: (check the solution) Implement the gradient descent. 

exo1;

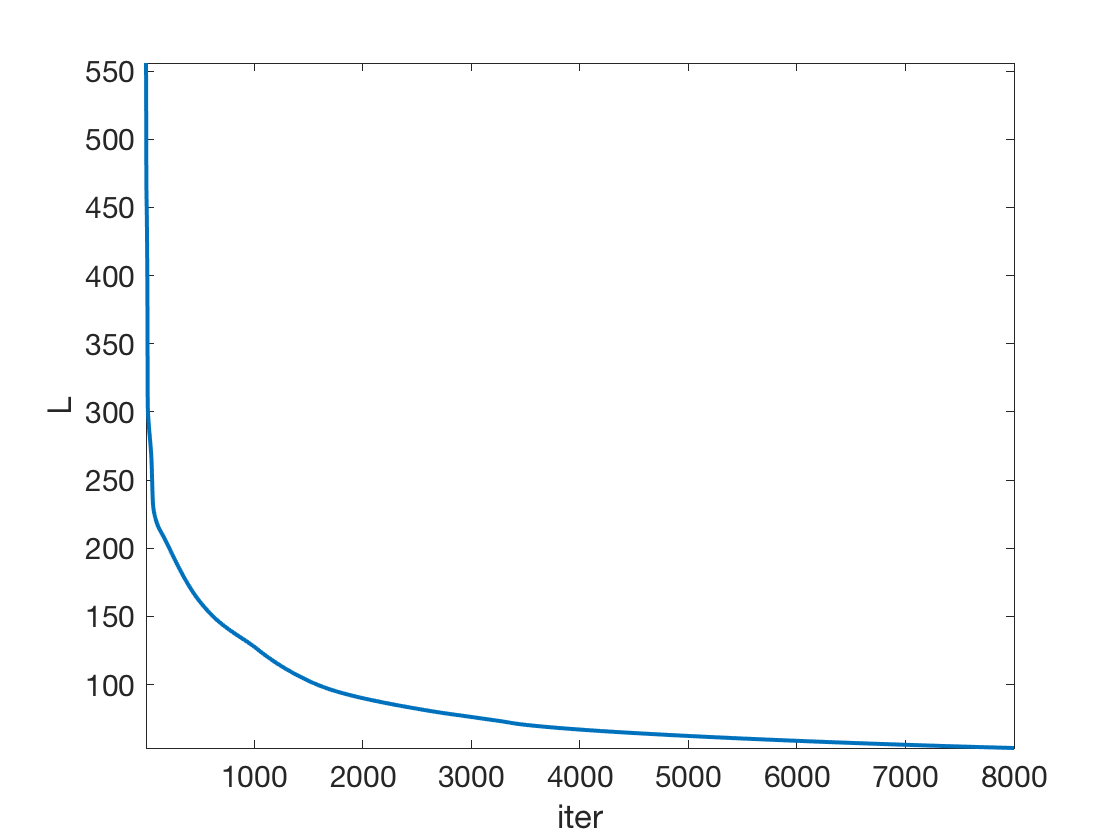
Grid for evaluation.

q = 100;
t = linspace(-1,1,q);
[Yg,Xg] = meshgrid(t,t);
Z = [Xg(:)';Yg(:)'];

Classification maps

V = EvalNN(Z,[], A,b,loss,rho);
U = reshape(SM(V{end}'), [q q k]);

Turn it into color.

col = [ [1 0 0]; [0 1 0]; [0 0 1]; [0 0 0]; [0 1 1]; [1 0 1]; [1 1 0]; ...
    [1 .5 .5]; [.5 1 .5]; [.5 .5 1]  ]';
R = zeros(q,q,3);
for i=1:k
    for a=1:3
        R(:,:,a) = R(:,:,a) + U(:,:,i) .* col(a,i);
    end
end

Final display of points and class probability.

clf;  hold on;
imagesc(t,t,permute(R, [2 1 3]));
for j=1:k
    I = find(y==j);
    plot(x(1,I), x(2,I), '.', 'color', col(:,j)*.8, 'MarkerSize', 20);
end
axis equal; axis off;

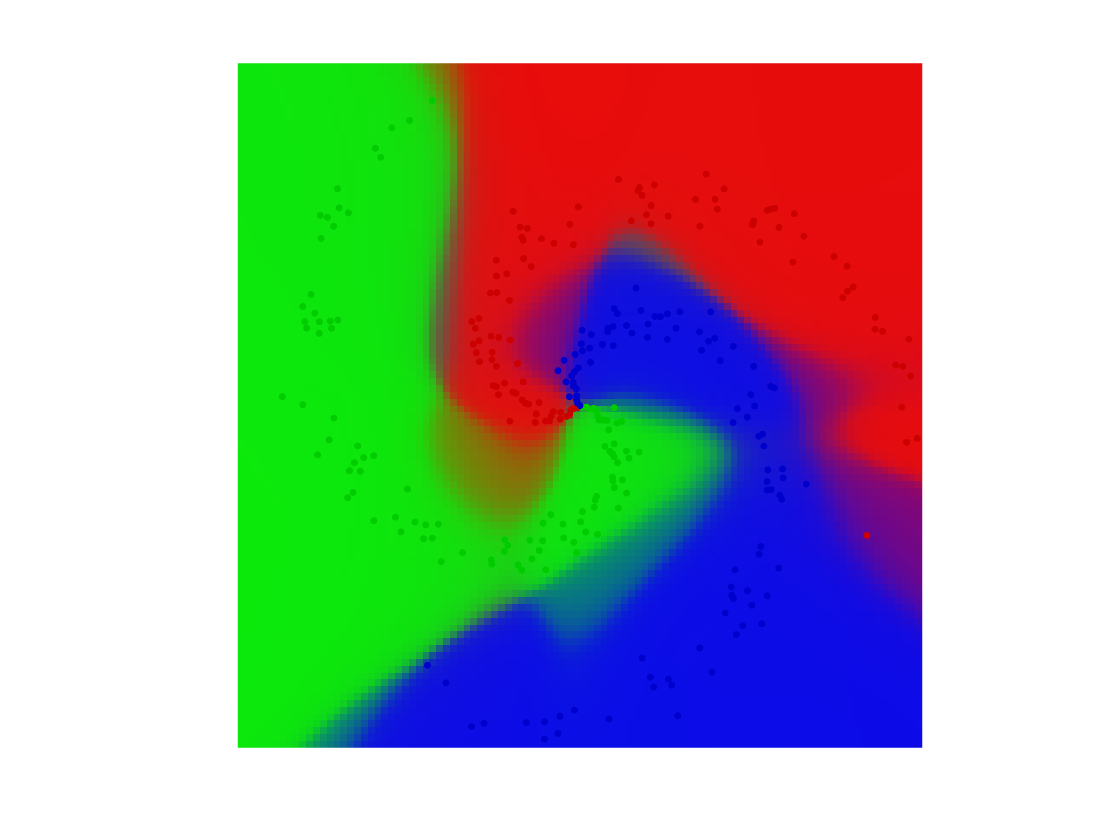
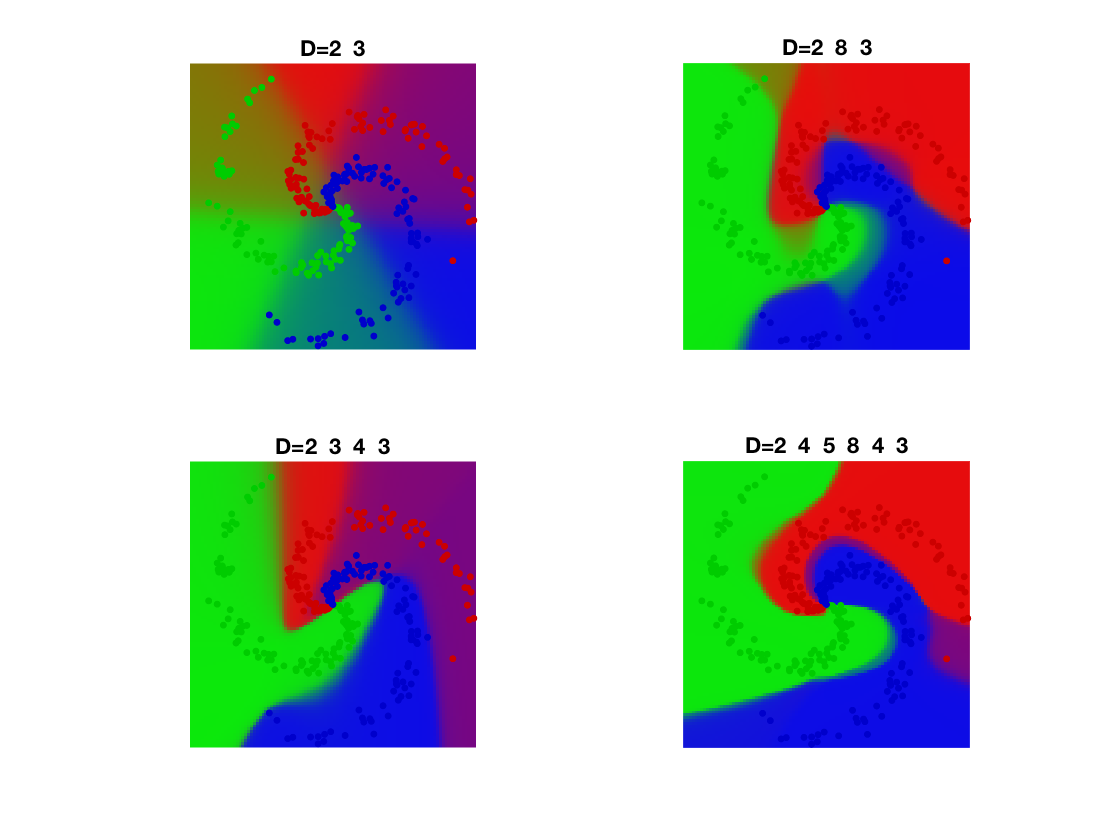
Exercice 2: (check the solution) Check the influence of the number of layers 

exo2;


Copyright (c) 2010 Gabriel Peyre