\[ \newcommand{\NN}{\mathbb{N}} \newcommand{\CC}{\mathbb{C}} \newcommand{\GG}{\mathbb{G}} \newcommand{\LL}{\mathbb{L}} \newcommand{\PP}{\mathbb{P}} \newcommand{\QQ}{\mathbb{Q}} \newcommand{\RR}{\mathbb{R}} \newcommand{\VV}{\mathbb{V}} \newcommand{\ZZ}{\mathbb{Z}} \newcommand{\FF}{\mathbb{F}} \newcommand{\KK}{\mathbb{K}} \newcommand{\UU}{\mathbb{U}} \newcommand{\EE}{\mathbb{E}} \newcommand{\Aa}{\mathcal{A}} \newcommand{\Bb}{\mathcal{B}} \newcommand{\Cc}{\mathcal{C}} \newcommand{\Dd}{\mathcal{D}} \newcommand{\Ee}{\mathcal{E}} \newcommand{\Ff}{\mathcal{F}} \newcommand{\Gg}{\mathcal{G}} \newcommand{\Hh}{\mathcal{H}} \newcommand{\Ii}{\mathcal{I}} \newcommand{\Jj}{\mathcal{J}} \newcommand{\Kk}{\mathcal{K}} \newcommand{\Ll}{\mathcal{L}} \newcommand{\Mm}{\mathcal{M}} \newcommand{\Nn}{\mathcal{N}} \newcommand{\Oo}{\mathcal{O}} \newcommand{\Pp}{\mathcal{P}} \newcommand{\Qq}{\mathcal{Q}} \newcommand{\Rr}{\mathcal{R}} \newcommand{\Ss}{\mathcal{S}} \newcommand{\Tt}{\mathcal{T}} \newcommand{\Uu}{\mathcal{U}} \newcommand{\Vv}{\mathcal{V}} \newcommand{\Ww}{\mathcal{W}} \newcommand{\Xx}{\mathcal{X}} \newcommand{\Yy}{\mathcal{Y}} \newcommand{\Zz}{\mathcal{Z}} \newcommand{\al}{\alpha} \newcommand{\la}{\lambda} \newcommand{\ga}{\gamma} \newcommand{\Ga}{\Gamma} \newcommand{\La}{\Lambda} \newcommand{\Si}{\Sigma} \newcommand{\si}{\sigma} \newcommand{\be}{\beta} \newcommand{\de}{\delta} \newcommand{\De}{\Delta} \renewcommand{\phi}{\varphi} \renewcommand{\th}{\theta} \newcommand{\om}{\omega} \newcommand{\Om}{\Omega} \renewcommand{\epsilon}{\varepsilon} \newcommand{\Calpha}{\mathrm{C}^\al} \newcommand{\Cbeta}{\mathrm{C}^\be} \newcommand{\Cal}{\text{C}^\al} \newcommand{\Cdeux}{\text{C}^{2}} \newcommand{\Cun}{\text{C}^{1}} \newcommand{\Calt}[1]{\text{C}^{#1}} \newcommand{\lun}{\ell^1} \newcommand{\ldeux}{\ell^2} \newcommand{\linf}{\ell^\infty} \newcommand{\ldeuxj}{{\ldeux_j}} \newcommand{\Lun}{\text{\upshape L}^1} \newcommand{\Ldeux}{\text{\upshape L}^2} \newcommand{\Lp}{\text{\upshape L}^p} \newcommand{\Lq}{\text{\upshape L}^q} \newcommand{\Linf}{\text{\upshape L}^\infty} \newcommand{\lzero}{\ell^0} \newcommand{\lp}{\ell^p} \renewcommand{\d}{\ins{d}} \newcommand{\Grad}{\text{Grad}} \newcommand{\grad}{\text{grad}} \renewcommand{\div}{\text{div}} \newcommand{\diag}{\text{diag}} \newcommand{\pd}[2]{ \frac{ \partial #1}{\partial #2} } \newcommand{\pdd}[2]{ \frac{ \partial^2 #1}{\partial #2^2} } \newcommand{\dotp}[2]{\langle #1,\,#2\rangle} \newcommand{\norm}[1]{|\!| #1 |\!|} \newcommand{\normi}[1]{\norm{#1}_{\infty}} \newcommand{\normu}[1]{\norm{#1}_{1}} \newcommand{\normz}[1]{\norm{#1}_{0}} \newcommand{\abs}[1]{\vert #1 \vert} \newcommand{\argmin}{\text{argmin}} \newcommand{\argmax}{\text{argmax}} \newcommand{\uargmin}[1]{\underset{#1}{\argmin}\;} \newcommand{\uargmax}[1]{\underset{#1}{\argmax}\;} \newcommand{\umin}[1]{\underset{#1}{\min}\;} \newcommand{\umax}[1]{\underset{#1}{\max}\;} \newcommand{\pa}[1]{\left( #1 \right)} \newcommand{\choice}[1]{ \left\{ \begin{array}{l} #1 \end{array} \right. } \newcommand{\enscond}[2]{ \left\{ #1 \;:\; #2 \right\} } \newcommand{\qandq}{ \quad \text{and} \quad } \newcommand{\qqandqq}{ \qquad \text{and} \qquad } \newcommand{\qifq}{ \quad \text{if} \quad } \newcommand{\qqifqq}{ \qquad \text{if} \qquad } \newcommand{\qwhereq}{ \quad \text{where} \quad } \newcommand{\qqwhereqq}{ \qquad \text{where} \qquad } \newcommand{\qwithq}{ \quad \text{with} \quad } \newcommand{\qqwithqq}{ \qquad \text{with} \qquad } \newcommand{\qforq}{ \quad \text{for} \quad } \newcommand{\qqforqq}{ \qquad \text{for} \qquad } \newcommand{\qqsinceqq}{ \qquad \text{since} \qquad } \newcommand{\qsinceq}{ \quad \text{since} \quad } \newcommand{\qarrq}{\quad\Longrightarrow\quad} \newcommand{\qqarrqq}{\quad\Longrightarrow\quad} \newcommand{\qiffq}{\quad\Longleftrightarrow\quad} \newcommand{\qqiffqq}{\qquad\Longleftrightarrow\qquad} \newcommand{\qsubjq}{ \quad \text{subject to} \quad } \newcommand{\qqsubjqq}{ \qquad \text{subject to} \qquad } \]

Basic Matlab/Scilab Instructions

Basic Matlab/Scilab Instructions

This tour shows some basics about Matlab/Scilab programming.

Contents

Installing toolboxes and setting up the path.

You need to download the following files: signal toolbox and general toolbox.

You need to unzip these toolboxes in your working directory, so that you have toolbox_signal and toolbox_general in your directory.

For Scilab user: you must replace the Matlab comment '%' by its Scilab counterpart '//'.

Recommandation: You should create a text file named for instance numericaltour.sce (in Scilab) or numericaltour.m (in Matlab) to write all the Scilab/Matlab command you want to execute. Then, simply run exec('numericaltour.sce'); (in Scilab) or numericaltour; (in Matlab) to run the commands.

Execute this line only if you are using Matlab.

getd = @(p)path(p,path); % scilab users must *not* execute this

Then you can add the toolboxes to the path.

getd('toolbox_signal/');
getd('toolbox_general/');

Comments

Matlab and Scilab are very similar languages. One of the main difference is that Matlab uses the character % to write comments, whereas Scilab uses the C-like syntax //. 

% this is a Matlab comment

It is thus very important, in all the numerical tours, to replace % comments by // comments if you are using Scilab.

Basic Matlab/Scilab commands.

The basic data is a 1D or 2D array.

a = 1; a = 2+1i; % real and complex numbers
b = [1 2 3 4]; % row vector
c = [1; 2; 3; 4]; % column vector
d = 1:2:7; % here one has d=[1 3 5 7]

You an acess one entry of an array, or select a sub-array by indexing.

% display the size
size(d)
% display the first entry
d(1)
% display the sub-array containing entries 1 and 2
d(1:2)

You can create pre-defined array using some basic functions

% identity, 1 and random matrices
A = eye(4,4);
B = ones(4,4);
C = rand(4,4);
% transpose
c = b';

The multiplication operator * is the matrix multiplication. To actually multiplies each entry of a vector, you need to use .*

% note the difference
D = C*A
D = C.*A
% You can apply functions to each entry of a matrix
E = A./C; % division
E = sin(A); % sinus is applied to each entry
E = abs(A + 1i*C); % modulus of each entry

You can modify matrices and arrays in various way.

b = sort(b); % sort values
b = b .* (b>2); % set to zeros (threshold) the values below 2
b(3) = []; % suppress the 3rd entry of a vector
B = [b; b]; % create a matrix of size 2x4
c = B(:,2); % to access 2nd column

Is is possible to access directly the last entry of a vector using the keyword end in Matlab and $ in Scilab. 

% The equivalent Scilab code is
%       b($-2:$) = 1;
b(end-2:end) = 1; % to access the last entries

% The equivalent Scilab code is
%       b = b($:-1:1);
b = b(end:-1:1); % reverse a vector

Advanced instructions

disp('Hello'); % display a text
x = 1.23456;
disp( sprintf('Value of x=%.2f', x) ); % print a values with 2 digits
A(A==Inf) = 3; % replace Inf values by 3
A(:); % flatten a matrix into a column vector
max(A(:)); % max of a matrix
% threshold to 0 values below .3.
C = C .* (abs(C)>.3);

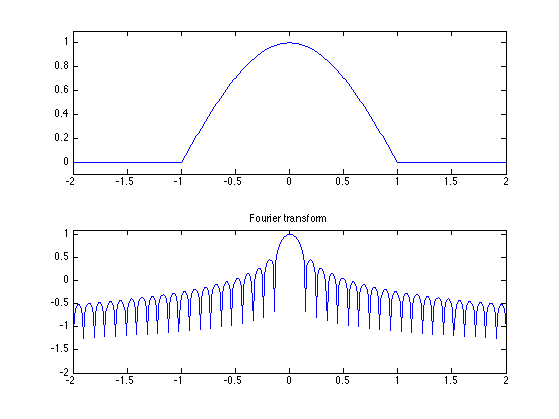
To display information of about a function, use the help command, for instance help perform_wavelet_transf.

Basic programming constructions include for, while and switch instructions. 

for i=1:3 % repeat the loop for i=1, i=2, i=3
    disp(i); % make here something
end
i = 3;
while i>0 % while syntax
    disp(i); % do smth
    i = i-1;
end

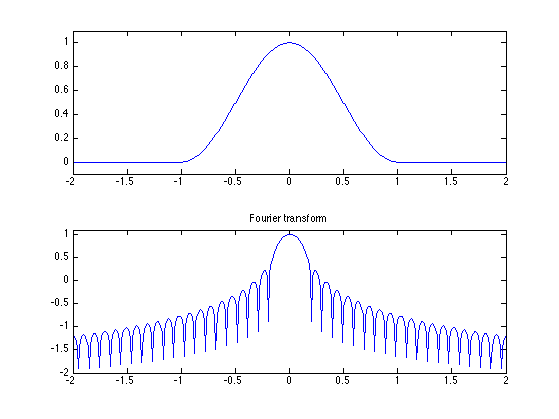
Load and visualize signals and images

Load and display an image (download function load_image.m should be in the toolboxes)

n = 256; % size of the image
M = load_image('lena', n);
clf;
imageplot(M);

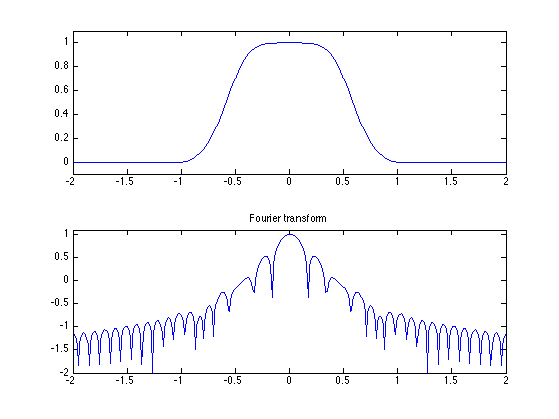
You can manipulate an image just like an arbitrary array

clf;
imageplot(M(1:50,1:50), 'Zoom', 1,2,1);
imageplot(-M, 'Reversed contrast', 1,2,2);


Copyright (c) 2010 Gabriel Peyre