\[ \newcommand{\NN}{\mathbb{N}} \newcommand{\CC}{\mathbb{C}} \newcommand{\GG}{\mathbb{G}} \newcommand{\LL}{\mathbb{L}} \newcommand{\PP}{\mathbb{P}} \newcommand{\QQ}{\mathbb{Q}} \newcommand{\RR}{\mathbb{R}} \newcommand{\VV}{\mathbb{V}} \newcommand{\ZZ}{\mathbb{Z}} \newcommand{\FF}{\mathbb{F}} \newcommand{\KK}{\mathbb{K}} \newcommand{\UU}{\mathbb{U}} \newcommand{\EE}{\mathbb{E}} \newcommand{\Aa}{\mathcal{A}} \newcommand{\Bb}{\mathcal{B}} \newcommand{\Cc}{\mathcal{C}} \newcommand{\Dd}{\mathcal{D}} \newcommand{\Ee}{\mathcal{E}} \newcommand{\Ff}{\mathcal{F}} \newcommand{\Gg}{\mathcal{G}} \newcommand{\Hh}{\mathcal{H}} \newcommand{\Ii}{\mathcal{I}} \newcommand{\Jj}{\mathcal{J}} \newcommand{\Kk}{\mathcal{K}} \newcommand{\Ll}{\mathcal{L}} \newcommand{\Mm}{\mathcal{M}} \newcommand{\Nn}{\mathcal{N}} \newcommand{\Oo}{\mathcal{O}} \newcommand{\Pp}{\mathcal{P}} \newcommand{\Qq}{\mathcal{Q}} \newcommand{\Rr}{\mathcal{R}} \newcommand{\Ss}{\mathcal{S}} \newcommand{\Tt}{\mathcal{T}} \newcommand{\Uu}{\mathcal{U}} \newcommand{\Vv}{\mathcal{V}} \newcommand{\Ww}{\mathcal{W}} \newcommand{\Xx}{\mathcal{X}} \newcommand{\Yy}{\mathcal{Y}} \newcommand{\Zz}{\mathcal{Z}} \newcommand{\al}{\alpha} \newcommand{\la}{\lambda} \newcommand{\ga}{\gamma} \newcommand{\Ga}{\Gamma} \newcommand{\La}{\Lambda} \newcommand{\Si}{\Sigma} \newcommand{\si}{\sigma} \newcommand{\be}{\beta} \newcommand{\de}{\delta} \newcommand{\De}{\Delta} \renewcommand{\phi}{\varphi} \renewcommand{\th}{\theta} \newcommand{\om}{\omega} \newcommand{\Om}{\Omega} \renewcommand{\epsilon}{\varepsilon} \newcommand{\Calpha}{\mathrm{C}^\al} \newcommand{\Cbeta}{\mathrm{C}^\be} \newcommand{\Cal}{\text{C}^\al} \newcommand{\Cdeux}{\text{C}^{2}} \newcommand{\Cun}{\text{C}^{1}} \newcommand{\Calt}[1]{\text{C}^{#1}} \newcommand{\lun}{\ell^1} \newcommand{\ldeux}{\ell^2} \newcommand{\linf}{\ell^\infty} \newcommand{\ldeuxj}{{\ldeux_j}} \newcommand{\Lun}{\text{\upshape L}^1} \newcommand{\Ldeux}{\text{\upshape L}^2} \newcommand{\Lp}{\text{\upshape L}^p} \newcommand{\Lq}{\text{\upshape L}^q} \newcommand{\Linf}{\text{\upshape L}^\infty} \newcommand{\lzero}{\ell^0} \newcommand{\lp}{\ell^p} \renewcommand{\d}{\ins{d}} \newcommand{\Grad}{\text{Grad}} \newcommand{\grad}{\text{grad}} \renewcommand{\div}{\text{div}} \newcommand{\diag}{\text{diag}} \newcommand{\pd}[2]{ \frac{ \partial #1}{\partial #2} } \newcommand{\pdd}[2]{ \frac{ \partial^2 #1}{\partial #2^2} } \newcommand{\dotp}[2]{\langle #1,\,#2\rangle} \newcommand{\norm}[1]{|\!| #1 |\!|} \newcommand{\normi}[1]{\norm{#1}_{\infty}} \newcommand{\normu}[1]{\norm{#1}_{1}} \newcommand{\normz}[1]{\norm{#1}_{0}} \newcommand{\abs}[1]{\vert #1 \vert} \newcommand{\argmin}{\text{argmin}} \newcommand{\argmax}{\text{argmax}} \newcommand{\uargmin}[1]{\underset{#1}{\argmin}\;} \newcommand{\uargmax}[1]{\underset{#1}{\argmax}\;} \newcommand{\umin}[1]{\underset{#1}{\min}\;} \newcommand{\umax}[1]{\underset{#1}{\max}\;} \newcommand{\pa}[1]{\left( #1 \right)} \newcommand{\choice}[1]{ \left\{ \begin{array}{l} #1 \end{array} \right. } \newcommand{\enscond}[2]{ \left\{ #1 \;:\; #2 \right\} } \newcommand{\qandq}{ \quad \text{and} \quad } \newcommand{\qqandqq}{ \qquad \text{and} \qquad } \newcommand{\qifq}{ \quad \text{if} \quad } \newcommand{\qqifqq}{ \qquad \text{if} \qquad } \newcommand{\qwhereq}{ \quad \text{where} \quad } \newcommand{\qqwhereqq}{ \qquad \text{where} \qquad } \newcommand{\qwithq}{ \quad \text{with} \quad } \newcommand{\qqwithqq}{ \qquad \text{with} \qquad } \newcommand{\qforq}{ \quad \text{for} \quad } \newcommand{\qqforqq}{ \qquad \text{for} \qquad } \newcommand{\qqsinceqq}{ \qquad \text{since} \qquad } \newcommand{\qsinceq}{ \quad \text{since} \quad } \newcommand{\qarrq}{\quad\Longrightarrow\quad} \newcommand{\qqarrqq}{\quad\Longrightarrow\quad} \newcommand{\qiffq}{\quad\Longleftrightarrow\quad} \newcommand{\qqiffqq}{\qquad\Longleftrightarrow\qquad} \newcommand{\qsubjq}{ \quad \text{subject to} \quad } \newcommand{\qqsubjqq}{ \qquad \text{subject to} \qquad } \]

Fluid Dynamics

Fluid Dynamics

This numerical tour explores fluid dynamics for image generation.

Contents

Installing toolboxes and setting up the path.

You need to download the following files: signal toolbox and general toolbox.

You need to unzip these toolboxes in your working directory, so that you have toolbox_signal and toolbox_general in your directory.

For Scilab user: you must replace the Matlab comment '%' by its Scilab counterpart '//'.

Recommandation: You should create a text file named for instance numericaltour.sce (in Scilab) or numericaltour.m (in Matlab) to write all the Scilab/Matlab command you want to execute. Then, simply run exec('numericaltour.sce'); (in Scilab) or numericaltour; (in Matlab) to run the commands.

Execute this line only if you are using Matlab.

getd = @(p)path(p,path); % scilab users must *not* execute this

Then you can add the toolboxes to the path.

getd('toolbox_signal/');
getd('toolbox_general/');

Velocity Flow Field

A velocity flow is simply a 2-D vector field \(V = (V_i)_{i=1}^N \in \RR^{n \times n \times 2}\) where \(V_i \in \RR^2\) is one of the \(N=n \times n\) vectors at a position indexed by \(i\).

It can be generated as a realization of Gaussian process. The blurring creates correlations in the flow.

n = 128;
options.bound = 'per';
V = perform_blurring(randn(n,n,2), 40, options);

Subsampling display operator.

myplot = @(V)plot_vf( V(1:6:n,1:6:n, :) );

We can display the vector field using arrow.

clf;
myplot(V);

We can renormalize the flow, which enhance the singularities. It defines \(\tilde V\) as \(\tilde V_i = V_i/\norm{V_i}\).

normalize = @(V)V ./ repmat( max(1e-9,sqrt(sum3(V.^2, 3))) , [1 1 2]);

Display.

clf;
myplot(normalize(V));

Incompressible Flows

An incompressible flow as vanishing divergence. The set of vector incompressible flow defines a sub-space of \(\RR^{n \times n \times 2}\) \[ \Ii = \enscond{V}{ \text{div}(V)=0 } \qwhereq \text{div}(V) = \pd{V}{x_1} + \pd{V}{x_2} \in \RR^{n \times n}. \] Here \(\pd{}{x_s}\) for \(s=1,2\) are finite differences approximation of the horizontal and vertical derivative operators (we suppose here periodic boundary conditions).

The orthogonal projection \(U = \text{Proj}_{\Ii}(V)\) on \(\Ii\) is computed by solving a Poisson equation \[ U = V-\nabla A \qwhereq \Delta A = \text{div}(V). \]

This is especially simple for periodic boundary conditions since \(A\) can be compute over the Fourier domain as \[ \forall \om \neq 0, \quad \hat A(\om) = \frac{\hat Y(\om)}{\mu(\om)} \qwhereq Y = \text{div}(V) \qandq \mu(\om_1,\om_2) = -4 \sin(\om_1 \pi / n)^2 -4 \sin(\om_2 \pi / n)^2 \] and \(\hat A(0)=0\).

Compute the kernel \(\mu(\om)\).

[Y,X] = meshgrid(0:n-1,0:n-1);
mu = sin(X*pi()/n).^2; mu = -4*( mu+mu' );
mu(1) = 1;

Computation of \(A\).

A = @(V)real( ifft2( fft2( div(V, options) ) ./ mu ) );

Projection on incompressible flows.

ProjI = @(V)V - grad(A(V), options);

Display \(U=\text{Proj}_{\Ii}(V)\).

U = ProjI(V);
clf;
myplot(U);

Display \(W=U-V\) the irrotational component of \(V\).

clf;
myplot(V-U);

Note that the decomposition \(V=U+W\) is called the Hoge decomposition of the vector field.

Image Advection Along the Flow

A flow defines a warping operator that transport the content of an image along the streaming of the flow.

We load an image \(f\).

name = 'lena';
f = crop( load_image(name, 2*n), n);

Given some vector field \(U\), the warping operator \(f_1 = \Ww_U(f)\) along the flow is define \[ f_1(x) = f(x+U(x)) \] i.e. it advects the values of \(f\) by the vector field \(U\) to obtain the values of \(f_1\).

We define \(U\) as a scaled normalized incompressible flow.

U = normalize(ProjI(V));

Helper function: enforce periodicity.

periodic = @(P)cat(3, mod(P(:,:,1)-1,n)+1, mod(P(:,:,2)-1,n)+1 );

Helper function: extend an image by 1 pixel to avoid boundary problems.

extend1 = @(f)[f f(:,1)];
extend = @(f)extend1(extend1(f)')';

Helper function: bilinear interpolation on a grid.

myinterp = @(P1,f1,Pi)interp2( P1(:,:,2), P1(:,:,1),f1, Pi(:,:,2), Pi(:,:,1) );

First we compute the initial and warped grids.

[Y,X] = meshgrid(1:n,1:n);
P = cat(3, X,Y);
[Y1,X1] = meshgrid(1:n+1,1:n+1);
P1 = cat(3, X1,Y1);

Defines the warping operator \(\Ww_U\).

W = @(f,U)myinterp( P1, extend(f), periodic( P - U ) );

Display a warped image \(\Ww_{\rho U}(f)\) for some scaling \(\rho\).

rho = 2;
clf;
imageplot(W(f,rho*U));

Exercice 1: (check the solution) Display \(\Ww_{\rho U}(f)\) for various values of \(\rho\). 

exo1;

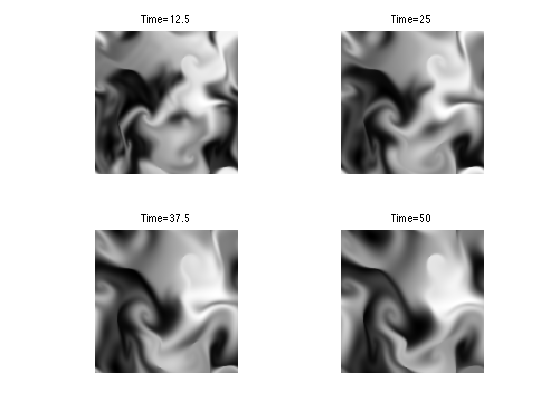
Exercice 2: (check the solution) Define an iterative scheme via: \[ f^{(\ell+1)} = \Ww_{\rho U}(f^{(\ell)}). \] Display the result \(f^{(\ell)}\), which corresponds approximately to solving an advection equation at time \(t=\ell \rho\). 

exo2;

Fluid Dynamics

Fluid dynamics solves the incompressible Navier-Stokes equations to evolve in time the vector field.

We discribe here a simple algorithm introduced in:

J. Stam, Stable Fluids, SIGGRAPH'99, 1999, p. 121-128.

It proposes a semi-implicit scheme for the resolution of the Navier Stockes equations for the movement of incompressible fluids \[ \pd{V}{t} = \text{Proj}_{\Ii}\pa{ -(V \cdot \nabla) V + \nu \Delta V + W }. \] Here \(\nu \geq 0\) is the viscosity of the fluid, \(W\) is a source term, \(\Delta\) is the Laplacian, and \(-(V \cdot \nabla) V\) is the non-linear self-advection, where we have used the short-hand notation \(V \cdot \nabla\) for the derivative operator along a flow \(V\): \[ (V \cdot \nabla)U = ( V_1 \pd{U_1}{x_1} + V_2 \pd{U_1}{x_2}, V_1 \pd{U_2}{x_1} + V_2 \pd{U_2}{x_2} ).\]

In order to visualize the flow, we also advect and diffuse along the flow a density \(g\) of particules, which is a scalar field. Once \(V\) has been computed, it follows a linear PDE \[ \pd{g}{t} = -(V \cdot \nabla) g + \mu \Delta g + h \] with some initial condition at time \(t=0\), where \(h\) is a source for the density.

In practice, we solve this PDE in parallel to the PDE for \(V\).

In the following, we use \(W=0\) and \(h=0\) (no sources).

Set the viscosity \(\nu\) for the velocity field.

nu = 1/10;

We use a larger viscosity \(\mu\) for the evolution of the density of particules.

mu = 2*nu;

Extend the warping operator \(\Ww_U\) to work with vector fields as input. This will apply \(\Ww_U\) on each channel of the vector field (X and Y coordinates). 

Wt = @(V,U)cat(3, W(V(:,:,1),U), W(V(:,:,2),U) );

We discretize the PDE's using some time step \(\tau\).

tau = .5;

The algorithm computes \(V^{(\ell)}\) at iteration \(\ell\) which is an approximation of the PDE solution at time \(\ell \tau\). It is computed itertatively as \[ \tilde V^{(\ell)} = \Ww_{\tau V^{(\ell)}}( V^{(\ell)} ) \qandq V^{(\ell+1)} = \text{Proj}_{\Ii}\pa{ \tilde V^{(\ell)} + \tau\nu\Delta \tilde V^{(\ell)} + \tau W } \]

It computes in parallel the evolution of the density as \[ \tilde g^{(\ell)} = \Ww_{\tau V^{(\ell)}}( g^{(\ell)} ) \qandq g^{(\ell+1)} = \tilde g^{(\ell)} + \tau\nu\Delta \tilde g^{(\ell)} + \tau h \]

Set the initial field \(V=V^{(0)}\) at time \(t=0\).

V = normalize(ProjI(V));

Set the initial density \(g=g^{(0)}\) at time \(t=0\).

g = f;

The first step is to advect the vector field \(V\) and \(g\) along the flow \(V\) itself. This corresponds to an implict discretization of the term \(-(V \cdot \nabla) V\). 

g = W (g,tau*U);
V = Wt(V,tau*U);

We implement the Laplacian using finite difference.

s1 = [2:n 1]; s2 = [n 1:n-1];
Delta = @(g)1/4 *( g(s1,:,:) + g(s2,:,:) + g(:,s1,:) + g(:,s2,:) ) - g;

The second step is to diffuse the vector field and the density.

V = V + tau*nu*Delta(V);
g = g + tau*mu*Delta(g);

The last step is to ensure incompressibility of \(V\) by projecting on \(\Ii\).

V = ProjI(V);

Exercice 3: (check the solution) Compute the fluid dynamic by iterating these steps. 

exo3;


Copyright (c) 2010 Gabriel Peyre