\[ \newcommand{\NN}{\mathbb{N}} \newcommand{\CC}{\mathbb{C}} \newcommand{\GG}{\mathbb{G}} \newcommand{\LL}{\mathbb{L}} \newcommand{\PP}{\mathbb{P}} \newcommand{\QQ}{\mathbb{Q}} \newcommand{\RR}{\mathbb{R}} \newcommand{\VV}{\mathbb{V}} \newcommand{\ZZ}{\mathbb{Z}} \newcommand{\FF}{\mathbb{F}} \newcommand{\KK}{\mathbb{K}} \newcommand{\UU}{\mathbb{U}} \newcommand{\EE}{\mathbb{E}} \newcommand{\Aa}{\mathcal{A}} \newcommand{\Bb}{\mathcal{B}} \newcommand{\Cc}{\mathcal{C}} \newcommand{\Dd}{\mathcal{D}} \newcommand{\Ee}{\mathcal{E}} \newcommand{\Ff}{\mathcal{F}} \newcommand{\Gg}{\mathcal{G}} \newcommand{\Hh}{\mathcal{H}} \newcommand{\Ii}{\mathcal{I}} \newcommand{\Jj}{\mathcal{J}} \newcommand{\Kk}{\mathcal{K}} \newcommand{\Ll}{\mathcal{L}} \newcommand{\Mm}{\mathcal{M}} \newcommand{\Nn}{\mathcal{N}} \newcommand{\Oo}{\mathcal{O}} \newcommand{\Pp}{\mathcal{P}} \newcommand{\Qq}{\mathcal{Q}} \newcommand{\Rr}{\mathcal{R}} \newcommand{\Ss}{\mathcal{S}} \newcommand{\Tt}{\mathcal{T}} \newcommand{\Uu}{\mathcal{U}} \newcommand{\Vv}{\mathcal{V}} \newcommand{\Ww}{\mathcal{W}} \newcommand{\Xx}{\mathcal{X}} \newcommand{\Yy}{\mathcal{Y}} \newcommand{\Zz}{\mathcal{Z}} \newcommand{\al}{\alpha} \newcommand{\la}{\lambda} \newcommand{\ga}{\gamma} \newcommand{\Ga}{\Gamma} \newcommand{\La}{\Lambda} \newcommand{\Si}{\Sigma} \newcommand{\si}{\sigma} \newcommand{\be}{\beta} \newcommand{\de}{\delta} \newcommand{\De}{\Delta} \renewcommand{\phi}{\varphi} \renewcommand{\th}{\theta} \newcommand{\om}{\omega} \newcommand{\Om}{\Omega} \renewcommand{\epsilon}{\varepsilon} \newcommand{\Calpha}{\mathrm{C}^\al} \newcommand{\Cbeta}{\mathrm{C}^\be} \newcommand{\Cal}{\text{C}^\al} \newcommand{\Cdeux}{\text{C}^{2}} \newcommand{\Cun}{\text{C}^{1}} \newcommand{\Calt}[1]{\text{C}^{#1}} \newcommand{\lun}{\ell^1} \newcommand{\ldeux}{\ell^2} \newcommand{\linf}{\ell^\infty} \newcommand{\ldeuxj}{{\ldeux_j}} \newcommand{\Lun}{\text{\upshape L}^1} \newcommand{\Ldeux}{\text{\upshape L}^2} \newcommand{\Lp}{\text{\upshape L}^p} \newcommand{\Lq}{\text{\upshape L}^q} \newcommand{\Linf}{\text{\upshape L}^\infty} \newcommand{\lzero}{\ell^0} \newcommand{\lp}{\ell^p} \renewcommand{\d}{\ins{d}} \newcommand{\Grad}{\text{Grad}} \newcommand{\grad}{\text{grad}} \renewcommand{\div}{\text{div}} \newcommand{\diag}{\text{diag}} \newcommand{\pd}[2]{ \frac{ \partial #1}{\partial #2} } \newcommand{\pdd}[2]{ \frac{ \partial^2 #1}{\partial #2^2} } \newcommand{\dotp}[2]{\langle #1,\,#2\rangle} \newcommand{\norm}[1]{|\!| #1 |\!|} \newcommand{\normi}[1]{\norm{#1}_{\infty}} \newcommand{\normu}[1]{\norm{#1}_{1}} \newcommand{\normz}[1]{\norm{#1}_{0}} \newcommand{\abs}[1]{\vert #1 \vert} \newcommand{\argmin}{\text{argmin}} \newcommand{\argmax}{\text{argmax}} \newcommand{\uargmin}[1]{\underset{#1}{\argmin}\;} \newcommand{\uargmax}[1]{\underset{#1}{\argmax}\;} \newcommand{\umin}[1]{\underset{#1}{\min}\;} \newcommand{\umax}[1]{\underset{#1}{\max}\;} \newcommand{\pa}[1]{\left( #1 \right)} \newcommand{\choice}[1]{ \left\{ \begin{array}{l} #1 \end{array} \right. } \newcommand{\enscond}[2]{ \left\{ #1 \;:\; #2 \right\} } \newcommand{\qandq}{ \quad \text{and} \quad } \newcommand{\qqandqq}{ \qquad \text{and} \qquad } \newcommand{\qifq}{ \quad \text{if} \quad } \newcommand{\qqifqq}{ \qquad \text{if} \qquad } \newcommand{\qwhereq}{ \quad \text{where} \quad } \newcommand{\qqwhereqq}{ \qquad \text{where} \qquad } \newcommand{\qwithq}{ \quad \text{with} \quad } \newcommand{\qqwithqq}{ \qquad \text{with} \qquad } \newcommand{\qforq}{ \quad \text{for} \quad } \newcommand{\qqforqq}{ \qquad \text{for} \qquad } \newcommand{\qqsinceqq}{ \qquad \text{since} \qquad } \newcommand{\qsinceq}{ \quad \text{since} \quad } \newcommand{\qarrq}{\quad\Longrightarrow\quad} \newcommand{\qqarrqq}{\quad\Longrightarrow\quad} \newcommand{\qiffq}{\quad\Longleftrightarrow\quad} \newcommand{\qqiffqq}{\qquad\Longleftrightarrow\qquad} \newcommand{\qsubjq}{ \quad \text{subject to} \quad } \newcommand{\qqsubjqq}{ \qquad \text{subject to} \qquad } \]

Geodesic Distance Computation on 3-D Meshes

Geodesic Distance Computation on 3-D Meshes

This tour explores the computation of the geodesic distance on a mesh using an iterative algorithm to solve the Eikonal equation.

Contents

Installing toolboxes and setting up the path.

You need to download the following files: signal toolbox, general toolbox, graph toolbox and wavelet_meshes toolbox.

You need to unzip these toolboxes in your working directory, so that you have toolbox_signal, toolbox_general, toolbox_graph and toolbox_wavelet_meshes in your directory.

For Scilab user: you must replace the Matlab comment '%' by its Scilab counterpart '//'.

Recommandation: You should create a text file named for instance numericaltour.sce (in Scilab) or numericaltour.m (in Matlab) to write all the Scilab/Matlab command you want to execute. Then, simply run exec('numericaltour.sce'); (in Scilab) or numericaltour; (in Matlab) to run the commands.

Execute this line only if you are using Matlab.

getd = @(p)path(p,path); % scilab users must *not* execute this

Then you can add the toolboxes to the path.

getd('toolbox_signal/');
getd('toolbox_general/');
getd('toolbox_graph/');
getd('toolbox_wavelet_meshes/');

Triangulated Mesh

We consider a 3-D surface discretized using a triangular mesh with \(N\) vertices. We denote \( \{x_i\}_{i=1}^{N} \) the set of vertices, where \(x_i \in \RR^3\). We denote \(\Ff \subset \{1, \ldots, N\}^3\) the set of faces.

First load a mesh.

name = 'beetle'; % 1k
name = 'camel'; % 600 v
name = 'cow'; % 700v
name = 'venus'; % 700 v
name = 'mannequin'; % 400 v
name = 'nefertiti'; % 300 v
[vertex0,faces0] = read_mesh(name);
clear options; options.name = name;

Display.

clf;
options.lighting = 1;
plot_mesh(vertex0,faces0,options);
shading('faceted');

Perform sub-division to obtained a finer mesh.

nsub = 2; % number of subdivision steps
options.sub_type = 'loop';
options.verb = 0;
[vertex,faces] = perform_mesh_subdivision(vertex0,faces0,nsub,options);
n = size(vertex,2);

Display.

clf;
options.lighting = 1;
plot_mesh(vertex,faces,options);
shading('faceted');

Useful shortcuts.

dotp = @(u,v)sum(u.*v,1);
R = @(u)reshape(u, [1 1 length(u)]);

Shortcut for the explicit inverse of a series of 2D matrices, and the multiplication with a vector.

Inv1 = @(M,d)[M(2,2,:)./d -M(1,2,:)./d; -M(2,1,:)./d M(1,1,:)./d];
Inv  = @(M)Inv1(M, M(1,1,:).*M(2,2,:) - M(1,2,:).*M(2,1,:));
Mult = @(M,u)[M(1,1,:).*u(1,1,:) + M(1,2,:).*u(2,1,:);  M(2,1,:).*u(1,1,:) + M(2,2,:).*u(2,1,:)];

Control Formulation of the Eikonal Equation

Our goal is to compute the geodesic distance to a set of starting points.

We consider an isotropic metric on the mesh \(W_i > 0\).

Given a set \(I\) of starting point, we want to compute the discrete geodesic distance map \( U \in \RR^N \) to the starting points \( \{x_i\}_{i \in I} \).

Let's consider a geodesic distance \(d(x,y)\) on a manifold. A general mathematical result is that the geodesic distance \[ d(x,A) = \umin{a \in A} d(x,a) \] to a set \(A\) is the unique solution to the following equation \[ \forall \, x \notin A, \quad d(x,A) = \umin{ y \in B(x) } d(y,A) + d(x,y) \] where \( B(x) \) is a small disk around \(x\) that does not contain \(A\).

In a discrete setting, one can use this property with \(B(x_i)\) being the one ring, made of the edges connecting vertices that are around \(x_i\). Using a piecewise linear interpolation of \(U\) on the mesh, one obtain that \(U\) is a solution to a fixed point equation \[ U = \Ga(U) \] where the update operator \( \Ga : \RR^N \rightarrow \RR^N \) is defined as \[ \Ga(U)_i = \umin{ (i,j,k) \in \Ff } d_{i,j,k} \] where \[ d_{i,j,k} = \umin{0 \leq t \leq 1} t U_{j} + (1-t) U_k + W_i \norm{ t x_j + (1-t) x_k - x }. \] The quantities \( d_{i,j,k} \) can in fact be computed by solving a second order polynomial, as we describe in the following section.

Geodesic distance Computation Using Jacobi Iterations

The mapping \(\Ga\) is monotone \[ U \leq V \qarrq \Ga(U) \leq \Ga(V). \] If one uses an initialization \(U^{(0)}\) such that \(\Ga(U^{(0)}) \geq U^{(0)} \) (for instance setting \(U^{(0)}=0\)), then the iterates \[ U^{(\ell+1)} = \Ga(U^{(\ell)}) \] are increasing. One can prove that they are bounded, and hence they converge to the (unique) fixed point solution of \(\Ga(U)=U\).

Define the metric \(W_i > 0\) on the mesh. We start with the uniform (constant) metric.

W = ones(n,1);

Indexes \(I \subset \{1,\ldots,N\}\) of starting points. Warning: this list works for the mesh nefertitit refined twice. For other meshes, use the function select3dtool to retrive the indexes of a few vertices. 

I = [88 2602 883 23];

Initialization of the distance map.

U = zeros(n,1);

Computation of the set of indexes for \(i,j,k\).

i = [faces(1,:) faces(2,:) faces(3,:) ];
j = [faces(2,:) faces(3,:) faces(1,:) ];
k = [faces(3,:) faces(1,:) faces(2,:) ];

x stores the position of all the \(x_i\) vertices (point where the value of \(d=d_{i,j,k}\) is computed), while x1 and x2 store respectively \(x_j-x_i\) and \(x_k-x_i\). 

x  = vertex(:,i);
x1 = vertex(:,j) - x;
x2 = vertex(:,k) - x;

ui stores \(U_{j}\), uk stores \(U_k\), w stores \(w=W_i\). We denote \(u=(U_j,U_k) \in \RR^2\). 

uj = U(j);
uk = U(k);
u = [R(uj); R(uk)];
w = R( W(i) );

C stores the inner product matrix \(C_{s,t} = \dotp{x_s}{x_t}\), and we denote \(S = C^{-1}\). 

C = [R(dotp(x1,x1)) R(dotp(x1,x2)); R(dotp(x2,x1)) R(dotp(x2,x2))];
S = Inv(C);

If we denote \(g = \al_1 x_1 + \al_2 x_2\) the (unknown) update direction, the geodesic distance (which is affine in the triangle), is written as \( U(z) = \dotp{g}{z-x} + d \) where \(d \in \RR\) is unknown.

We need to compute both \(g\) and \(d\). Since \(U(x_j)=u_1\) and \(U(x_k)=u_2\), one obtains \[ \al = S ( u - d \mathbb{I} ), \] where \(\mathbb{I} = (1,1) \in \RR^2\). Making use of the Eikonal equation \( \norm{\nabla U(x)} = \norm{g} = w \), one obtains that \(d\) is the (maximum) solution of the following second order equation \[ a d^2 - 2 b d + c = 0 \qwhereq \choice{ a = \dotp{S \mathbb{I}}{\mathbb{I}} \\ b = \dotp{S \mathbb{I}}{u} \\ c = \dotp{S u}{u} - w^2 } \]

Compute the values of \(a, b, c\).

a = sum(sum(S));
b = dotp( sum(S,2), u );
c = dotp( Mult(S,u), u ) - w.^2;

Compute the reduced discriminant \(\de = b^2 - a c\), which is always positive.

delta = max( b.^2 - a.*c, 0);

The solution is then \[ d = \frac{ b + \sqrt{\delta} }{ a }. \]

d = (b + sqrt(delta) )./a;

To ensure correctness of the scheme, the update should come from within the triangle (which correspond to the condition \[t \in [0,1]\] in the original definition of \(d_{i,j,k}\) using the control formulation). This corresponds to having \( \al_1<=0 \) and \(\al_2 \leq 0\) where \( \al = S ( u - d \mathbb{I} ) \).

Compute \(\al \in \RR^2\).

alpha = Mult( S, u - repmat(d, 2, 1) );

For the index \(i \in J\) where the update comes from outside the edge \( [x_j,x_k] \), we use an update along the edge \[ d = \min\pa{ U_j + \norm{x-x_j}W_i, U_k + \norm{x-x_k}W_i }. \] 

J = find( alpha(1,1,:)>0 | alpha(2,1,:)>0 );
d1 = sqrt(dotp(x1,x1)); d1 = d1(:).*w(:) + uj(:);
d2 = sqrt(dotp(x2,x2)); d2 = d2(:).*w(:) + uk(:);
d = d(:);
d(J) = min(d1(J), d2(J));

Now that d stores the value of d_{i,j,k} for a bunch of faces assign in U1(i) the mininimum between the previous U1(i) and all the entries in d that corresponds to a face \((i,j,k)\). 

U1 = accumarray(i', d, [n 1], @min);  U1(U1==0) = Inf;

Enforce the boundary conditions \(\forall i \in I, \, U_i = 0\).

U1(I) = 0;

Update the solution.

U = U1;

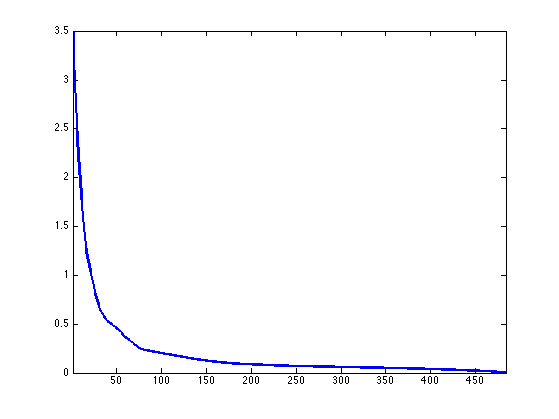
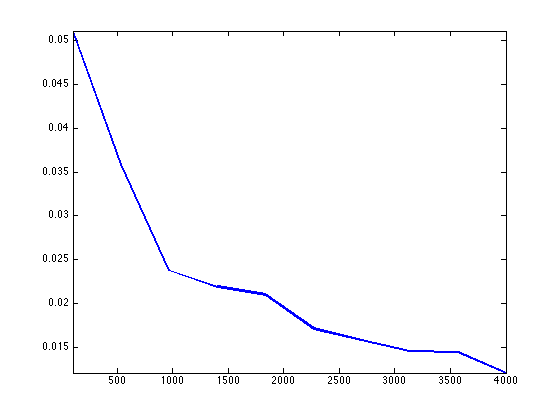
Exercice 1: (check the solution) Perform the full iterative algorithm until convergence. Store in err(l) the fixed point error \( \norm{ U^{(\ell+1)} - U^{(\ell)} } \). Note: you might want to put outside of the loop all the quantities that do not depend on \(u\), e.g. \(S, a, \) etc. 

exo1;

Display the fixed point energy.

clf;
h = plot(err);
set(h, 'LineWidth', 2);
axis tight;

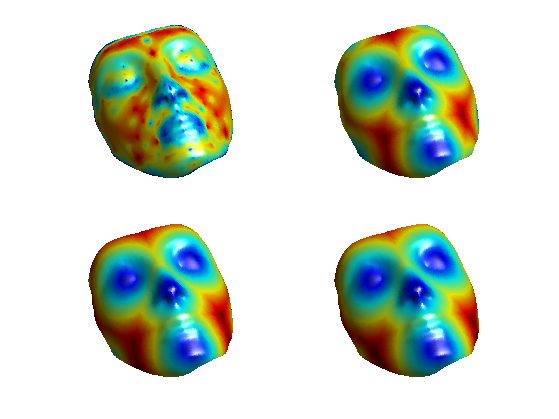
For the display of the distance.

mycolor = @(U,k)mod(U/max(U), 1/k);
mycolor = @(U,k)cos(2*pi*k*U/max(U));

Display the distance map.

clf;
options.face_vertex_color = mycolor(U, 5);
plot_mesh(vertex,faces,options);
colormap jet(256);
shading interp;

Geodesic Path Extraction

A geodesic minimal path from any point on the mesh to the starting point can be computed using a gradient descent. Since the computed geodesic distance is affine on each triangle, it makes sense to define a discretized path that is a line segment on each face.

Extract minimal paths from all over the mesh, starting from the boundary.

k = 30;
pend = round(rand(k,1)*n)+1;
options.method = 'continuous';
paths = compute_geodesic_mesh(U, vertex, faces, pend, options);

Display.

clf;
plot_fast_marching_mesh(vertex,faces, mycolor(U, 5), paths, options);

Geodesic Distance Convergence

The discrete geodesic distance converges to the continuous distance when the mesh is refined.

Compute a Delaunay triangulation of random point on a square with the first point in the center.

n = 3000;
vertex = [2*rand(2,n)-1; zeros(1,n)];
vertex(:,1) = 0;
faces = compute_delaunay(vertex);
options.name = '';
I = 1;

Display.

clf
plot_mesh(vertex,faces);
shading faceted;

Exercice 2: (check the solution) Compute and display the geodesic distance. 

exo2;

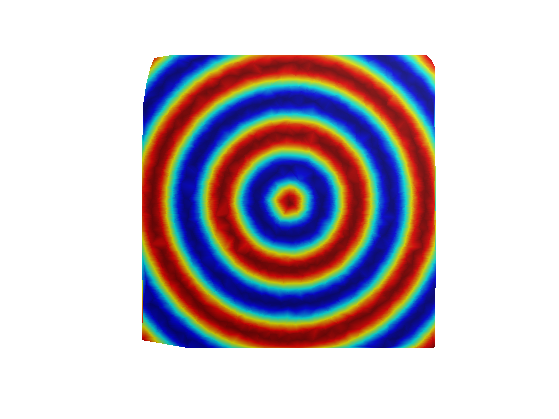
Exercice 3: (check the solution) Display the convergence of the computed geodesic distance to the the true geodesic distance (which is the Euclidean distance \( \norm{x_i} \)) as \(n\) increases. Note: the triangulation with increasing number of points should be refining (i.e. a finer triangulation should contains all the other ones). 

exo3;

Spacially Varying Metrics

One can define a non-constant metric on the mesh.

Triangulation of a square.

n = 8000;
vertex = [rand(2,n); zeros(1,n)];
vertex(:,1) = [0 .3 0]';
faces = compute_delaunay(vertex);
I = 1;

Generate a binary metric in order to produce a reflexion effect.

W = ones(n,1);
W(vertex(1,:)<.5) = 1/2;

Display the metric.

options.face_vertex_color = W;
clf;
plot_mesh(vertex,faces,options);
colormap jet(256);

Exercice 4: (check the solution) Compute the geodesic distance for a metric \(W_i\) that is not constant over the mesh. 

exo4;


Copyright (c) 2010 Gabriel Peyre