\[ \newcommand{\NN}{\mathbb{N}} \newcommand{\CC}{\mathbb{C}} \newcommand{\GG}{\mathbb{G}} \newcommand{\LL}{\mathbb{L}} \newcommand{\PP}{\mathbb{P}} \newcommand{\QQ}{\mathbb{Q}} \newcommand{\RR}{\mathbb{R}} \newcommand{\VV}{\mathbb{V}} \newcommand{\ZZ}{\mathbb{Z}} \newcommand{\FF}{\mathbb{F}} \newcommand{\KK}{\mathbb{K}} \newcommand{\UU}{\mathbb{U}} \newcommand{\EE}{\mathbb{E}} \newcommand{\Aa}{\mathcal{A}} \newcommand{\Bb}{\mathcal{B}} \newcommand{\Cc}{\mathcal{C}} \newcommand{\Dd}{\mathcal{D}} \newcommand{\Ee}{\mathcal{E}} \newcommand{\Ff}{\mathcal{F}} \newcommand{\Gg}{\mathcal{G}} \newcommand{\Hh}{\mathcal{H}} \newcommand{\Ii}{\mathcal{I}} \newcommand{\Jj}{\mathcal{J}} \newcommand{\Kk}{\mathcal{K}} \newcommand{\Ll}{\mathcal{L}} \newcommand{\Mm}{\mathcal{M}} \newcommand{\Nn}{\mathcal{N}} \newcommand{\Oo}{\mathcal{O}} \newcommand{\Pp}{\mathcal{P}} \newcommand{\Qq}{\mathcal{Q}} \newcommand{\Rr}{\mathcal{R}} \newcommand{\Ss}{\mathcal{S}} \newcommand{\Tt}{\mathcal{T}} \newcommand{\Uu}{\mathcal{U}} \newcommand{\Vv}{\mathcal{V}} \newcommand{\Ww}{\mathcal{W}} \newcommand{\Xx}{\mathcal{X}} \newcommand{\Yy}{\mathcal{Y}} \newcommand{\Zz}{\mathcal{Z}} \newcommand{\al}{\alpha} \newcommand{\la}{\lambda} \newcommand{\ga}{\gamma} \newcommand{\Ga}{\Gamma} \newcommand{\La}{\Lambda} \newcommand{\Si}{\Sigma} \newcommand{\si}{\sigma} \newcommand{\be}{\beta} \newcommand{\de}{\delta} \newcommand{\De}{\Delta} \renewcommand{\phi}{\varphi} \renewcommand{\th}{\theta} \newcommand{\om}{\omega} \newcommand{\Om}{\Omega} \renewcommand{\epsilon}{\varepsilon} \newcommand{\Calpha}{\mathrm{C}^\al} \newcommand{\Cbeta}{\mathrm{C}^\be} \newcommand{\Cal}{\text{C}^\al} \newcommand{\Cdeux}{\text{C}^{2}} \newcommand{\Cun}{\text{C}^{1}} \newcommand{\Calt}[1]{\text{C}^{#1}} \newcommand{\lun}{\ell^1} \newcommand{\ldeux}{\ell^2} \newcommand{\linf}{\ell^\infty} \newcommand{\ldeuxj}{{\ldeux_j}} \newcommand{\Lun}{\text{\upshape L}^1} \newcommand{\Ldeux}{\text{\upshape L}^2} \newcommand{\Lp}{\text{\upshape L}^p} \newcommand{\Lq}{\text{\upshape L}^q} \newcommand{\Linf}{\text{\upshape L}^\infty} \newcommand{\lzero}{\ell^0} \newcommand{\lp}{\ell^p} \renewcommand{\d}{\ins{d}} \newcommand{\Grad}{\text{Grad}} \newcommand{\grad}{\text{grad}} \renewcommand{\div}{\text{div}} \newcommand{\diag}{\text{diag}} \newcommand{\pd}[2]{ \frac{ \partial #1}{\partial #2} } \newcommand{\pdd}[2]{ \frac{ \partial^2 #1}{\partial #2^2} } \newcommand{\dotp}[2]{\langle #1,\,#2\rangle} \newcommand{\norm}[1]{|\!| #1 |\!|} \newcommand{\normi}[1]{\norm{#1}_{\infty}} \newcommand{\normu}[1]{\norm{#1}_{1}} \newcommand{\normz}[1]{\norm{#1}_{0}} \newcommand{\abs}[1]{\vert #1 \vert} \newcommand{\argmin}{\text{argmin}} \newcommand{\argmax}{\text{argmax}} \newcommand{\uargmin}[1]{\underset{#1}{\argmin}\;} \newcommand{\uargmax}[1]{\underset{#1}{\argmax}\;} \newcommand{\umin}[1]{\underset{#1}{\min}\;} \newcommand{\umax}[1]{\underset{#1}{\max}\;} \newcommand{\pa}[1]{\left( #1 \right)} \newcommand{\choice}[1]{ \left\{ \begin{array}{l} #1 \end{array} \right. } \newcommand{\enscond}[2]{ \left\{ #1 \;:\; #2 \right\} } \newcommand{\qandq}{ \quad \text{and} \quad } \newcommand{\qqandqq}{ \qquad \text{and} \qquad } \newcommand{\qifq}{ \quad \text{if} \quad } \newcommand{\qqifqq}{ \qquad \text{if} \qquad } \newcommand{\qwhereq}{ \quad \text{where} \quad } \newcommand{\qqwhereqq}{ \qquad \text{where} \qquad } \newcommand{\qwithq}{ \quad \text{with} \quad } \newcommand{\qqwithqq}{ \qquad \text{with} \qquad } \newcommand{\qforq}{ \quad \text{for} \quad } \newcommand{\qqforqq}{ \qquad \text{for} \qquad } \newcommand{\qqsinceqq}{ \qquad \text{since} \qquad } \newcommand{\qsinceq}{ \quad \text{since} \quad } \newcommand{\qarrq}{\quad\Longrightarrow\quad} \newcommand{\qqarrqq}{\quad\Longrightarrow\quad} \newcommand{\qiffq}{\quad\Longleftrightarrow\quad} \newcommand{\qqiffqq}{\qquad\Longleftrightarrow\qquad} \newcommand{\qsubjq}{ \quad \text{subject to} \quad } \newcommand{\qqsubjqq}{ \qquad \text{subject to} \qquad } \]

Rank Filters for Image Processing

Rank Filters for Image Processing

This numerical tour explores non-linear local filters that proceeds by ordering the pixels in a neighboorhood and selecting a given ranked entry.

Contents

Installing toolboxes and setting up the path.

You need to download the following files: signal toolbox and general toolbox.

You need to unzip these toolboxes in your working directory, so that you have toolbox_signal and toolbox_general in your directory.

For Scilab user: you must replace the Matlab comment '%' by its Scilab counterpart '//'.

Recommandation: You should create a text file named for instance numericaltour.sce (in Scilab) or numericaltour.m (in Matlab) to write all the Scilab/Matlab command you want to execute. Then, simply run exec('numericaltour.sce'); (in Scilab) or numericaltour; (in Matlab) to run the commands.

Execute this line only if you are using Matlab.

getd = @(p)path(p,path); % scilab users must *not* execute this

Then you can add the toolboxes to the path.

getd('toolbox_signal/');
getd('toolbox_general/');

Continuous Rank Filtering

We consider an image \(f : [0,1]^2 \rightarrow \RR\).

For any \(\beta \in [0,1]\), we define the rank filter \(\phi_\be^B\) of order \(\beta\) associated to a set \(B\) to be \[ g = \phi_\beta^B(f) \qwhereq g(x) = \inf \: \enscond{t \in \RR}{ \mu( f^{-1}(]-\infty,t]) \cap x+B ) \geq \mu(B)/2 }. \] where \(\mu\) is the Lebesgue measure on \(\RR\).

One usually assumes that \(B\) is the ball of radius \(\epsilon>0\) \[ B = B_\epsilon = \enscond{x}{\norm{x} \leq \epsilon}. \]

When \(\be=0\) (resp. \(\be=1\), resp. \(\be=1/2\)), then \(g(x)\) is the miniminimum (resp. maximum, resp. median) value of \(f\) in a small neighboorhood of radius \(\epsilon\) \[ \phi_0^{B_\epsilon}(f)(x) = \umin{\norm{y-x} \leq \epsilon} f(y), \] \[ \phi_{1/2}^{B_\epsilon}(f)(x) = \umax{\norm{y-x} \leq \epsilon} f(y), \] \[ \phi_{1}^{B_\epsilon}(f)(x) = \underset{\norm{y-x} \leq \epsilon}{\text{median}} f(y). \]

The operator \(\phi_\beta^B\) is contrast-invariant, meaning that it computes with increasing functions \( \psi : \RR \rightarrow \RR \) \[ \phi_\beta^B \circ \psi = \psi \circ \phi_\beta^B. \] The axiomatic study of contrast invariant operator was initiated in the comunity of mathematical morphology, see [Matheron75], [Tukey77], [Serra82].

Note also that there exist generalization of rank filters (and in particular the median filter) to vector valued images \( f : [0,1]^2 \rightarrow \RR^d\). Since the notion of rank does not exists anymore, one has to rely on variational caracteriation of the median, see for instance [CasSapChu00].

The medial filtering is the most popular rank filter. It is particularly efficient to remove impulse noise, see for instance [Piterbarg84], [FanHall94]. See also [AriasDon99] for a theoritical analysis of median filtering and of a two-stage iterated version.

Patches in Images

We apply rank filters to discretized images by interpreting them as piecewise constant functions.

Size \(N = n \times n\) of the image.

n = 256;

We load an image \(f_0 \in \RR^N\).

name = 'hibiscus';
f0 = load_image(name, n);
f0 = rescale(crop( sum(f0,3) ,n));

Display \(f_0\).

clf;
imageplot(f0);

Noise level \(\si\).

sigma = .04;

Generate a noisy image \(f=f_0+\epsilon\) where \(\epsilon \times \Nn(0,\si^2\text{Id}_N)\).

f = f0 + randn(n,n)*sigma;

Display \(f\).

clf;
imageplot(clamp(f));

For simplicity, we consider the case where the set \(B\) is a square of \(w_1 \times w_2\) pixels. where we denote \(w\) to be the half width of the patches, and \(w_1=2w+1\) the full width. 

w = 3;
w1 = 2*w+1;

We define the patch extraction operator \[ p = p_x(f) \in \RR^{w_1 \times w_1} \qwhereq \forall -w \leq s_1,s_2 \leq w, \quad p(s) = f(x+s). \]

We now define the function \(\Pi(f) = (p_x(f))_x \) that extracts all possible patches.

We set up large \((n,n,w_1,w_1)\) matrices to index the the X and Y position of the pixel to extract.

[Y,X] = meshgrid(1:n,1:n);
[dY,dX] = meshgrid(-w:w,-w:w);
dX = reshape(dX, [1 1 w1 w1]);
dY = reshape(dY, [1 1 w1 w1]);
X = repmat(X, [1 1 w1 w1]) + repmat(dX, [n n 1 1]);
Y = repmat(Y, [1 1 w1 w1]) + repmat(dY, [n n 1 1]);

We handle boundary condition by reflexion

X(X<1) = 2-X(X<1); Y(Y<1) = 2-Y(Y<1);
X(X>n) = 2*n-X(X>n); Y(Y>n) = 2*n-Y(Y>n);

Patch extractor operator \(\Pi\).

Pi = @(f)reshape( f(X + (Y-1)*n), [n n w1*w1] );

We store the patches \(\Pi(f)\) as a \(n \times n \times w_1^2\) matrix \(P\) such that, for each pixel \(x\), \(P(x)\) is a vector of size \(w_1^2\) storing the entries of \(p_x(f)\). 

P = Pi(f);

Display some example of patches

clf;
for i=1:16
    x = floor( rand*(n-1)+1 );
    y = floor( rand*(n-1)+1 );
    imageplot( reshape(P(x,y,:,:), w1,w1), '', 4,4,i );
end

Linear Filter

A linear filter (convolution) can be computed using this patch representation as \[ g(x) = \sum_{i} \la_i p_x(f)_i. \]

In the case where \(\la_i=1/w_1^2\), this defines the mean value inside the patch: \[ g(x) = \frac{1}{w_1^2} \sum_{i} p_x(f)_i. \] 

Pmean = @(f)mean(Pi(f),3);

Display it.

clf;
imageplot(Pmean(f));

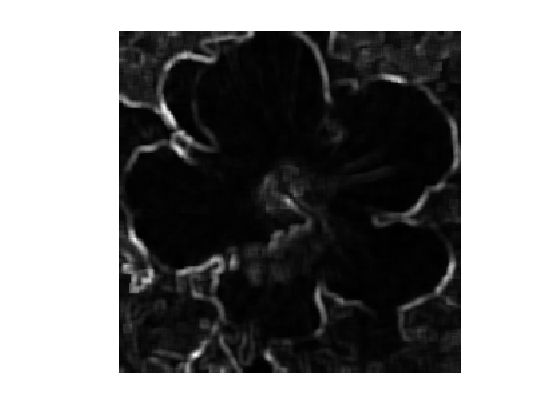
Note that this is not a rank filter (this a linear filter) and that it is not contrast invariant. This is shown by displaying \[ \phi_\beta^B(f) - \psi^{-1} \circ \phi_\beta^B \circ \psi(f) \] which is non-zero. 

p = 100;
psi = @(f)f.^(1/p);
ipsi = @(f)f.^p;
imageplot(Pmean(abs(f)) - ipsi(Pmean(psi(abs(f)))));

Opening and Closing Rank Filters

We now come back to the discrete computation of a rank filter \(\phi_\be^B\) for \(B\) a square of width \(w_1 \times w_1\) pixels.

It is defined as \(g=\phi_\beta^B(f)\) where \[ g(x) = \text{rank}_{r(\beta)}( p_x(f) ) \] where \(\text{rank}_r(v)\) extracted the element of order \(k\) in the sorted value of \(v \in \RR^Q\) (here \(Q=w_1^2\)). More precisely, we denote \[ v_{\si(1)} \leq v_{\si(2)} \leq \ldots \leq v_{\si(Q)} \] where \(\si \in \Sigma_Q\) is an ordering permutation, which can be computed in \( O(N \log(N)) \) operations with the QuickSort algorithm. Then the ranked valued is \[ \text{rank}_r(v) = v_{\si(r)}. \]

In order to be consistent with the continuous definition of the rank filter, one should define the rank as \[ r=r(\beta) = \lfloor Q r \rfloor. \] 

r = @(beta)min(ceil(beta*w1*w1)+1,w1*w1);

Shortcut for the rank filter.

subsample = @(x,s)x(:,:,s);
phi = @(f,beta)subsample(sort(Pi(f), 3), r(beta));

Exercice 1: (check the solution) Compute the rank filter for several values of \(\beta\). 

exo1;

The case \(\beta=0\) corresponds to the closing operator from mathematical morphology (min filter).

closing = @(f)phi(f,0);
clf;
imageplot(closing(f));

The case \(\beta=1\) corresponds to the opening operator from mathematical morphology (max filter).

opening = @(f)phi(f,1);
clf;
imageplot(opening(f));

Exercice 2: (check the solution) Compute a closing followed by an opening. 

exo2;

Exercice 3: (check the solution) Compute an opening followed by a closing. 

exo3;

Exercice 4: (check the solution) Perform iterated opening and closing. 

exo4;

Median Filter

The median filter corresponds to the case where \(\be=1/2\).

medfilt = @(f)phi(f,1/2);

Display the result.

clf;
imageplot(medfilt(f));

Iterated median filtering computes \[ f^{(\ell+1)} = \phi_{1/2}^B( f^{(\ell)} ). \] As already mentionned, one can show that a properly

In the case where \(f\) is of class \(C^3\) and \(\nabla f(x) \neq 0\), one has the following Taylor expansion \[ \phi_{1/2}^{B_\epsilon}(x) = f(x) + \frac{\epsilon^2}{6} \norm{\nabla f(x)} \text{Curv}(f)(x) + O(\epsilon^{7/3}) \] where the curvature operator is \[ \text{Curv}(f) = \text{div}\pa{ \frac{\nabla f}{\norm{\nabla f}} }. \]

Intuitively, it means that if one iterates the operator \( \phi_{1/2}^{B_\epsilon} \) with a proper re-scaling \(\ell \leftrightarrow t\) and when \(\epsilon \rightarrow 0\), then \(f^{(\ell)}\) tends to the solution to the famous mean-curvature motion PDE \[ \pd{f}{t} = \norm{\nabla f} \text{Curv}(f). \]

This conjecture was initially mentionned in [BeMerOsh92]. This was rigorously proved in [Ishii95], [BarGeorg], [Evans93] using the machinery of viscosity solutions.

Similar result holds for other class of contrast invariant operator, see for instance [Cao98] for affine invariant operators, and [GuiMoRy04] for an axiomatic and general framework.

Exercice 5: (check the solution) Perform iterated median filtering, and store the output in f1. 

exo5;

Display.

clf;
imageplot(f1);

Bibliography


Copyright (c) 2010 Gabriel Peyre